Deo zbornika Učimo algoritme

Algoritmi pretrage

Algoritam pretraživanja je algoritam koji daje rješenje nekog problema nakon evaluacije skupa mogućih rješenja. Skup svih mogućih rješenja problema naziva se “prostor pretraživanja”.

Osnovna podjela algoritama pretraživanja je na:

• “slijepe” (eng. blind, uninformed search) i
• “usmjerene” (engl. directed, informed search)

Slijepo pretraživanje

Strategija slijepog pretraživanja ne uzima u obzir specifičnu prirodu problema. Na taj način “slijepi” algoritmi pretraživanja mogu se poopćiti, odnosno na isti način mogu se primjeniti na široko područje problema. Međutim većina prostora pretraživanja je vrlo velika, te ovakvi algoritmi nisu efikasni osim za male primjere (većinom za edukacijske svrhe).

Slijepo pretraživanje napreduje sistematski kroz prostor pretraživanja ili po nekom prethodno definiranom redoslijedu ili birajući redoslijed evaluacije slučajno.

Pretraživanje liste (niza)

Ovo je najjednostavnija vrsta algoritma pretraživanja. Cilj je pronaći određeni element prema nekom ključu - element koji ima određenu vrijednost ili sadrži informaciju povezanu sa ključem.

To je jedan od najčešćih problema u računalstvu, pa je složenost i struktura ovakvih algoritama temeljito proučena. Najjednostavniji takav algoritam je linearno pretraživanje, koje jednostavno sekvencijalno ispituje jedan po jedan element iz liste. Vrijeme izvođenja je dugačko, ali ovaj algoritam se može direktno primjeniti na “neobrađenu” listu, za razliku od algoritama koji npr. zahtijevaju da lista bude sortirana.

Binarno pretraživanje započinje na polovici liste i nastavlja se stalnim raspolavljanjem intervala u kojem bi se mogao naći traženi zapis. Prosječni broj pretraživanja je log₂ n-1, gdje je n broj elemenata u listi. Za binarno pretraživanje lista mora biti sortirana i mora biti omogućen direktan pristup svim elementima liste (što je važno kod npr. pretraživanja slogova datoteke).

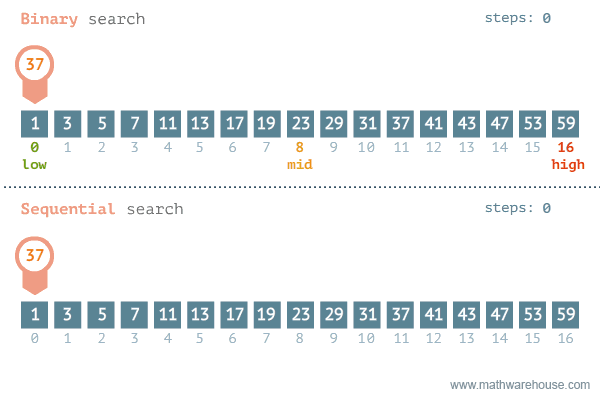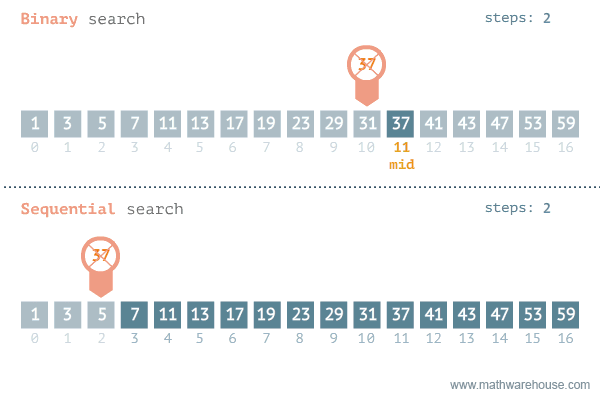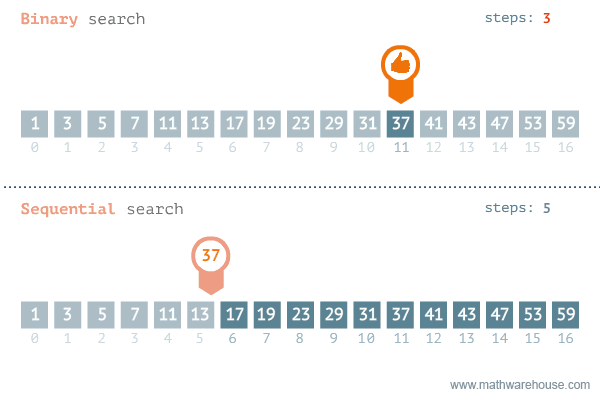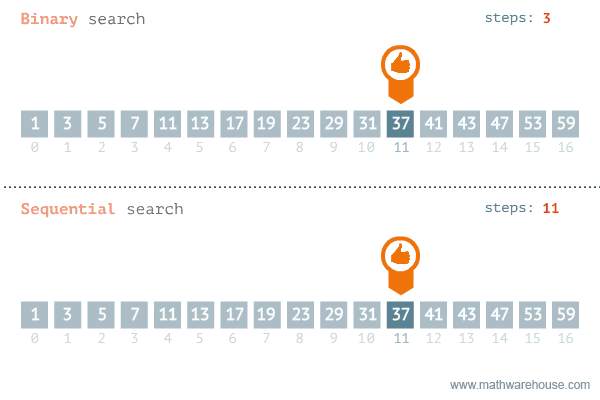
Za vrlo velike liste efikasniji je algoritam interpolacijskog pretraživanja.

Pretraživanje stabla

Algoritmi pretraživanja strukture stabla čine jezgru tehnika pretraživanja. Pretražuju se čvorovi stabla koji se uzimaju iz strukture podataka te se generiraju njihovi sljedbenici i dodaju u strukturu. Struktura reda koristi se za čuvanje generiranih i još neistraženih čvorova. Redoslijed kojim se čvorovi pohranjuju u red za ispitivanje i uklanjanje određuje tip pretraživanja.

Postoje dva osnovna načina pretraživanja strukture stabla:

• Pretraživanje u širinu (engl. breadth-first search) - ispituju se svi čvorovi na određenoj razini prije prelaska na slijedeću razinu.
• Pretraživanje u dubinu (engl. depth-first search) - pretražuje poniranjem niz stablo što je brže moguće tako da uvijek generira djecu zadnjeg proširenog čvora dok ne dođe do rješenja (ili dok ne pređe zadani limit dubine).

Algoritam pretraživanja u dubinu razlikuje se od onog u širinu po redoslijedu kojim je taj čvor stavljen u red - novostvorena djeca stavljaju se na početak reda tako da se ona prva ispituju.

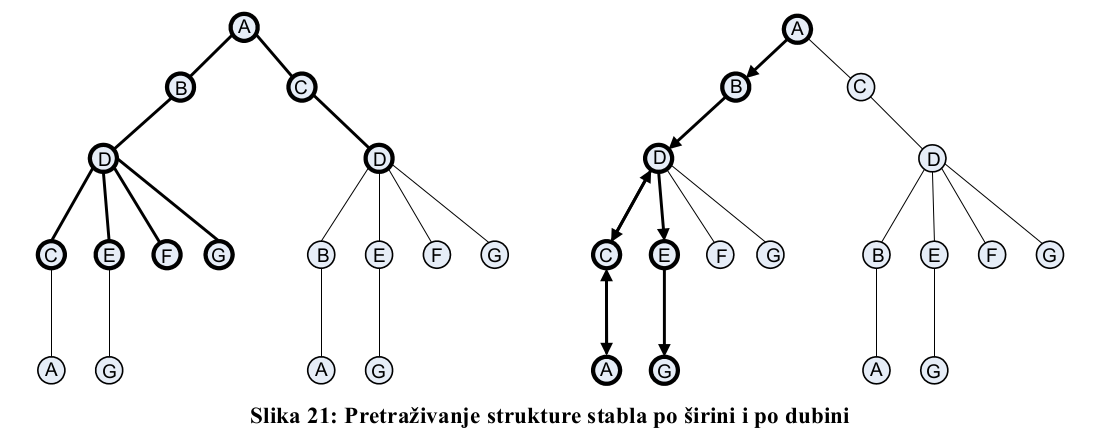
Za pretraživanje strukture grafa također postoji nekoliko algoritama, a neki od njih zapravo su proširenja algoritama za pretraživanje strukture stabla.

Usmjereno pretraživanje

Za razliku od slijepog pretraživanja, usmjereno pretraživanje koristi informacije o naravi problema kao vodilje koje mogu bitno ubrzati pronalaženje rješenja - što je više podataka dostupno postupku pretraživanja to je pretraživanje efikasnije. Takve informacije obično se nazivaju heurističke – temelje se na iskustvenim pravilima i tehnikama prosuđivanja koje mogu pomoći, ali nužno ne osiguravaju pronalaženje rješenja. Heurističke informacije mogu se oblikovati u heurističku evaluacijsku funkciju koja zavisi od pojedinog čvora i od cilja koji se traži.

Većina algoritama za usmjereno pretraživanje namijenjena je za strukture stabla, npr. algoritam “najboljeg prvog” (eng. best-first search) koji zadržava procjene vrijednosti heurističkih funkcija svih prethodno generiranih čvorova i izabire najbolji za nastavak potrage.

Svi mogući potezi u nekoj igri (npr. šah ili “križić – kružić”, tj. “iks – oks”) mogu se prikazati strukturom stabla. Takva struktura prikazuje prostor mogućih stanja koja nastupaju tijekom igre. Pretraživanje takve strukture u svrhu pronalaženja efikasne strategije planiranja slijedećih poteza dodatno je otežano jer treba razmatrati i sve moguće poteze koje može povući drugi igrač. Računalni programi za ovakve namjene pripadaju u domenu umjetne inteligencije. Osnovne vrste algoritama za pretraživanje u ovakvoj vrsti problema su: minimax algoritam, search tree pruning i alpha-beta pruning (en. pruning – kresati, očistiti).

Slika 22 sadrži samo mali dio ukupnog prostora mogućih stanja u igri “križić – kružić”, tj. na svakoj razini nakon druge “ekspandiran” je samo jedan čvor (prikazani su sljedbenici samo jednog čvora stabla), makar i svi ostali čvorovi te razine imaju isti broj sljedbenika.

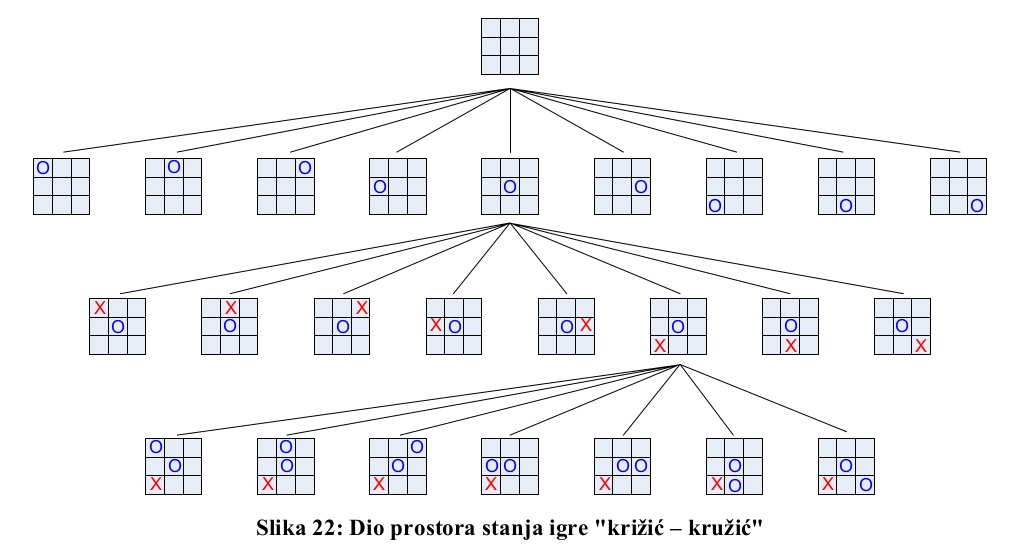
U većini sličnih prostora stanja izražen je problem tzv. “kombinatoričke eksplozije”, tj. sa svakim novim elementom uzetim u obzir, eksponencijalno raste broj mogućih kombinacija odnosno stanja koje treba pretraživati.

Izvor: N. Pavković, D. Marjanović, N. Bojčetić, Programiranje i algoritmi, skripta II, Zagreb, 2005.