Deo zbornika Učimo algoritme

Binarna pretraga

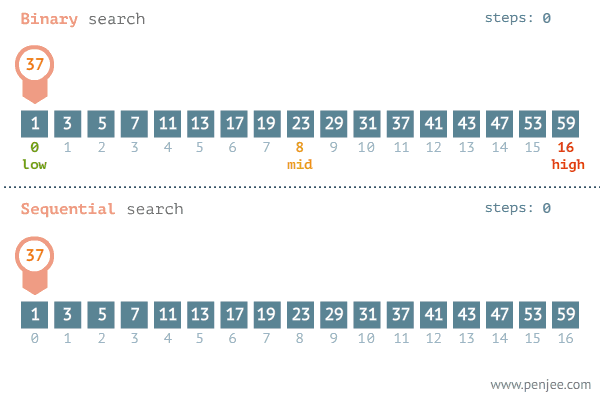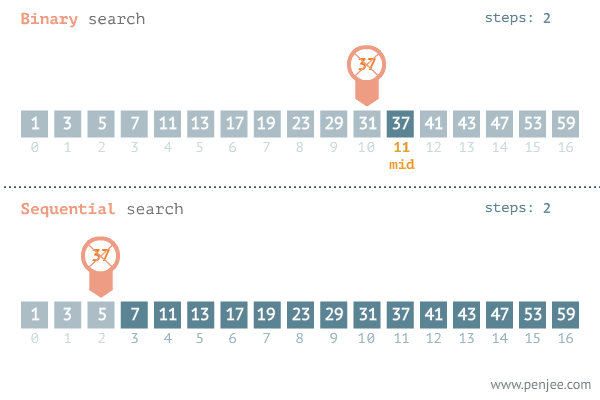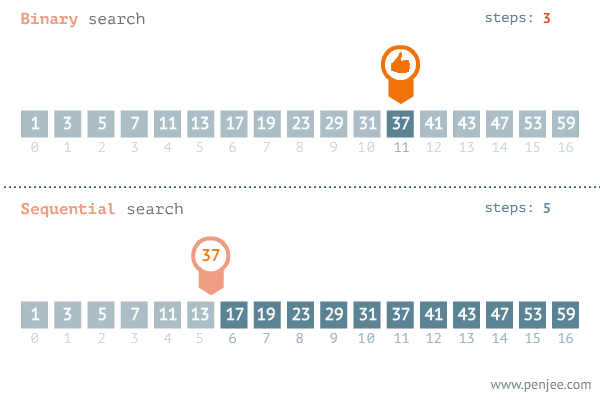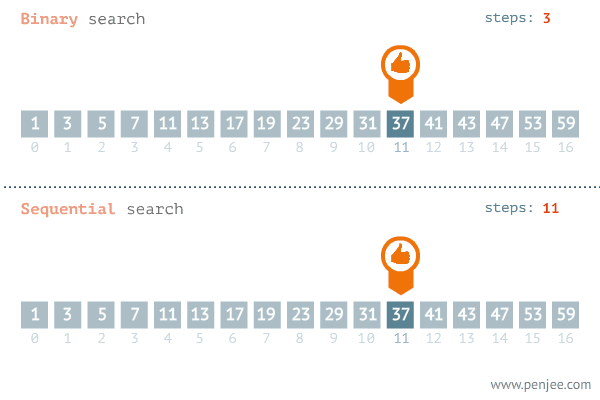
Binarna pretraga je efikasan algoritam za nalaženje elementa u sortiranom nizu. Umesto da proverava svaki element redom, binarna pretraga u svakom koraku deli skup na pola.

Pretraživanje se vrši na sledeći način: nalazi srednji element skupa, proverava je li jednak traženoj vrednosti, ako jeste vraća njegov indeks, ako nije pretraga se nastavlja nad podskupom manjih (ako je srednji element veći od tražene vrednosti) ili većih elemenata (ako je srednji element manji).

Vremenska složenost binarne pretrage je O(log n) - logaritamska složenost. Binarno pretraživanje je primer podeli-i-vladaj algoritama. Može se implementirati iterativno ili rekurzivno.

Uređenost podataka

Binarno pretraživanje je daleko efikasnije nego linearno, ali zahteva da su podaci koje pretražuje uređeni. Ovo je jedan od glavnih razloga zašto se reči u rečnicima, enciklopedijama i imenicima sortiraju. Oni se obično pretražuju postupkom koji odgovara varijantama binarne pretrage. Efikasnost postaje još očiglednija ukoliko zamislimo koliko bi komplikovano bilo pretraživanje reči redom u nesortiranom rečniku.

Rekurzivna implementacija

Naredna funkcija daje rekurzivnu implementaciju binarnog pretraživanja. Poziv binarna_pretraga(a, l, d, x) vraća indeks elementa niza a između l i d (uključujući i njih) koji je jednak zadatoj vrednosti x ako postoji, inače -1. Dakle, ukoliko se želi pretraga celog niza, funkciju treba pozvati sa binarna_pretraga(a, 0, n-1, x).

int binarna_pretraga(int a[], int l, int d, int x) {
  int s;

  if (l > d)
    return -1;
  s = l + (d - l)/2;
  if (x > a[s])
    return binarna_pretraga(a, s+1, d, x);
  else if (x < a[s])
    return binarna_pretraga(a, l, s-1, x);
  else
    return s;
}

Primetimo da se za nalaženje središta, umesto izraza l + (d - l)/2 može koristiti i kraći izraz (l + d)/2. Ipak, upotreba prvog izraza je preporučena kako bi se smanjila mogućnost nastanka prekoračenja. Ovo je jedan od mnogih nizu primera gde izrazi koji su matematički jednaki, pokazuju različita svojstva u aritmetici fiksirane širine.

Složenost ove funkcije je O(log n), a njena korektnost se dokazuje jednostavno.

Iterativna implementacija

Oba rekurzivna poziva u prethodnoj funkciji su bila repno-rekurzivna, tako da se mogu jednostavno eliminisati. Time se dobija iterativna funkcija koja vraća indeks elementa niza a koji je jednak zadatoj vrednosti x ako takva postoji, inače -1.

int binarna_pretraga(int a[], int n, int x) {
  int l, d, s;

  l = 0; d = n-1;
  while(l <= d) {
    s = l + (d - l)/2;
    if (x > a[s])
      l = s + 1;
    else if (x < a[s])
      d = s - 1;
    else
      return s;
  }
  return -1;
}

Literatura

• Predrag Janičić i Filip Marić, PROGRAMIRANJE 2, Osnove programiranja kroz programski jezik C, Matematički fakultet, Beograd, 2017.