Složenost algoritama

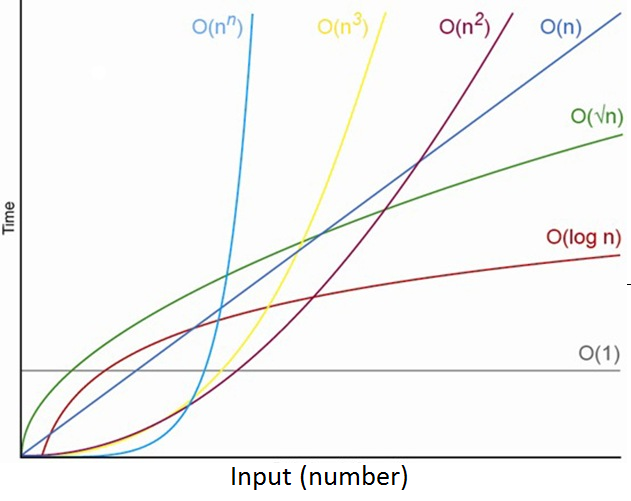
Kada pišemo neku proceduru, veoma je bitno da procenimo koliko je ona složena. Složenost se meri brojem operacija koje neki algoritam obavlja. Složenost je direktno proporcionalna trajanju, a obrnuto proporcionalna efikasnosti algoritma. Složeni algoritmi su spori i neefikasni. Cilj je rešiti problem u što manje koraka.

Zanimljivo da je kod većine algoritama prvi utisak vara. Oni algoritmi koji krenu brže kasnije uspore, i obratno. Tek kod veoma velikih unosa, krivulja rasta postaje izraženija.

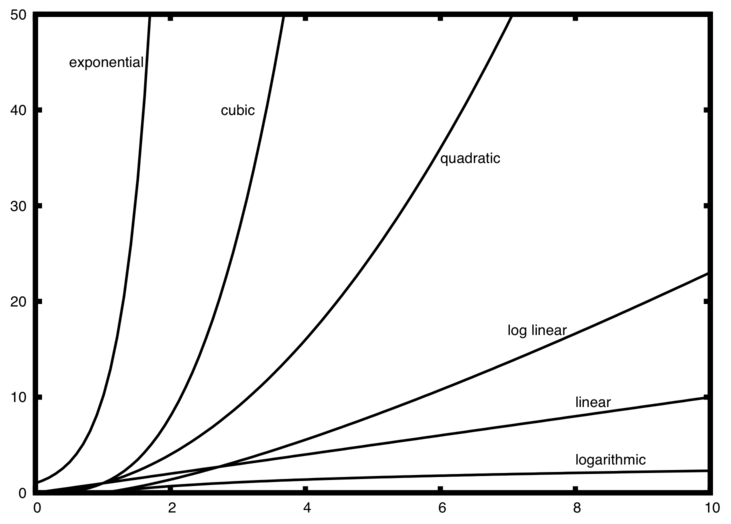
Glavni resursi koje algoritam zahteva su procesorsko vreme i prostor u memoriji. Kada govorimo o složenosti, uglavnom nas brine vremenska složenost, a prostorna samo izuzetno.

Konstantna složenost: 1

vreme uvek isto, nezavisno od unosa

Algoritmi konstantne složenosti izvode uvek isti broj operacija, bez obzira na veličinu unosa. Dobar primer je uzimanje nasumičnog člana niza. Dužina niza ne utiče na složenost, jer svakom članu pristupamo jednako brzo.

Ovako izgleda funkcija koja prima niz, a vraća nasumični član:

niz => niz[Math.floor(Math.random() * niz.length)]

Logaritamska (podlinearna) složenost: log n

vreme raste sporije od unosa

Algoritmi logaritamske složenosti su vrlo efikasni algoritmi, čije vreme izvršenja raste znatno sporije od rasta unosa.

Reč logaritam podseća na algoritam, ali nemaju nikakve veze. Logaritam je operacija suprotna stepenovanju. Pošto se u računarstvu podrazumeva osnova 2, logaritam je operacija neprekidnog deljenja na pola.

Logaritamski algoritmi nakon svakog koraka eliminišu polovinu preostalog skupa. Najpoznatiji primer logaritamske složenosti je binarna pretraga, koja u svakom prolasku deli sortirani niz na pola, i odbacuje jednu polovinu.

Primer iz stvarnog sveta je traženje reči u rečniku. Logaritam od 1.000.000 (milion) iznosi 19,9, što znači da u ogromnom rečniku od milion reči možemo pronaći bilo koju reč u najviše 20 koraka.

U klasu podlinearnih algoritama spadaju i algoritmi korenske složenosti, koji su veoma retki.

Linearna složenost: n

vreme raste isto kao unos

Algoritam ima linearnu složenost kada nad svakim članom ulaza obavlja isti broj operacija (može i samo jednu). Na primer:

for (let i = 0; i < 100; i++) {  
    console.log(i)
}

Količina rada po elementu je konstantna i ne zavisi od veličine unosa. Vreme izvršenja srazmerno je količini unosa.

Primer iz stvarnog sveta bilo bi čitanje knjige :)

Kvadratna složenost: n^2

vreme raste unos na kvadrat

Kod kvadratnih algoritama količina rada po svakom elementu zavisi od ukupnog broja elemenata. Svaki od n unosa zahteva n količinu rada, pa je ukupan broj prolazaka jednak unosu na kvadrat. Klasičan primer je petlja unutar petlje:

const brojUnosa = 100
let brojProlazaka = 0

for(i = 0; i < brojUnosa; i++){
  for(j = 0; j < brojUnosa; j++){
    brojProlazaka++
  }
}
// brojProlazaka je 10000

Jedna od praktičnih primena je kombinacija svakog elementa sa svakim:

const osobe = ["Ana", "Milovan", "Azra", "Senad", "Petra", "Petar"]

for(let i = 0; i < osobe.length; i++){
  for(let j = i+1; j < osobe.length; j++){
    console.log(osobe[i], osobe[j])
  }
}

Ako imamo 3 petlje jednu unutar druge, onda imamo O(n^3) odnosno kubnu složenost.

Eksponencijalna složenost: x^n

vreme raste na stepen unosa

Kod eksponencijalnih algoritama svako uvećenje unosa uvećava vreme izvršenja za jedan stepen. Ako na primer, za jedan unos imamo 10 operacija, za dva unosa 10 * 10, već za tri unosa imamo 10 * 10 * 10 operacija.

Primer eksponencijalne složenosti je naivna rekurzija za zbir fibonačijevih brojeva:

const fibonaci = n => {
  if (n < 3) return 1
  return fibonaci(n - 1) + fibonaci(n - 2)
}

Takođe, pokušaj nalaženja lozinke putem svim mogućih kombinacija.