Eratostenovo sito

Eratostenovo sito (takođe Eratostenovo rešeto) je algoritam koji pronalazi sve proste brojeve u rasponu od 1 do N. Osmislio ga je starogrčki naučnik i upravnik Aleksandrijske biblioteke Eratosten.

Algoritam radi na nizu brojeva od 1 do N. Na početku, iz niza uklanja broj jedan, jer on po definiciji nije prost. Nakon toga, algoritam uzima sljedeći broj u nizu (broj 2), označava ga da je prost i iz niza uklanja sve njegove sadržioce (tj. brojeve djeljive sa 2), jer sigurno nisu prosti. Zatim se ponovo uzima sljedeći broj koji nije izbačen (broj 3) i uklanjaju se svi njegovi sadržioci. Obzirom da je broj 4 uklonjen iz niza, jer je djeljiv sa 2, algoritam će uzeti broj 5. Ovaj postupak će se ponavljati i na kraju će u nizu ostati samo prosti brojevi.

Kada implementiramo Eratostenovo sito, dovoljno je obraditi brojeve koji su manji ili jednaki √N. Dakle, ako tražimo proste brojeve od 1 do 100, dovoljno je da iz niza izbacimo sadržioce brojeva koji su manji ili jednaki 10.

Koraci algoritma

Predstavićemo rad algoritma koji traži sve proste brojeve od 1 do 100. Na početku imamo niz u kojem se nalaze svi brojevi od 1 do 100.

Korak 1

Na početku ćemo izbaciti broj 1, jer po definiciji nije prost. Nakon toga, obilježavamo broj 2 kao prost, i izbacijemo sve njegove sadržioce.

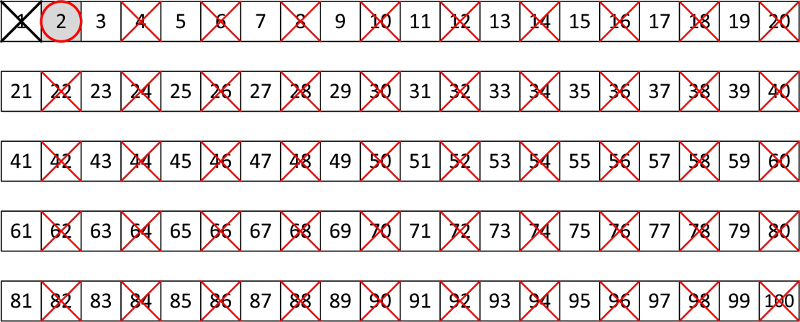
Korak 2

Sljedeći broj koji nije izbačen je 3. Algoritam ga označava da je prost i izbacuje sve njegove sadržioce.

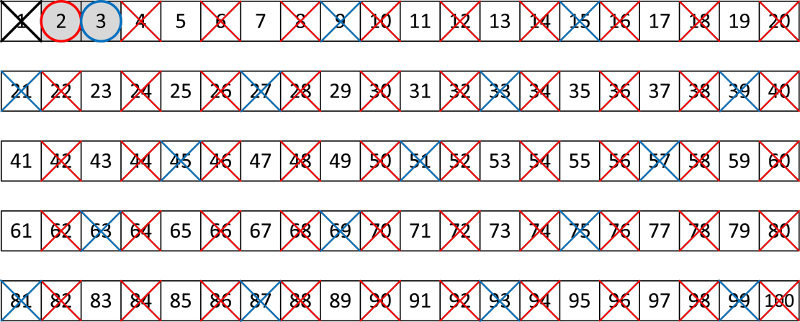
Korak 3

Broj 4 je ranije izbačen, tako da algoritam uzima broj 5 označava ga da je prost i izbacuje sve njegove sadržioce.

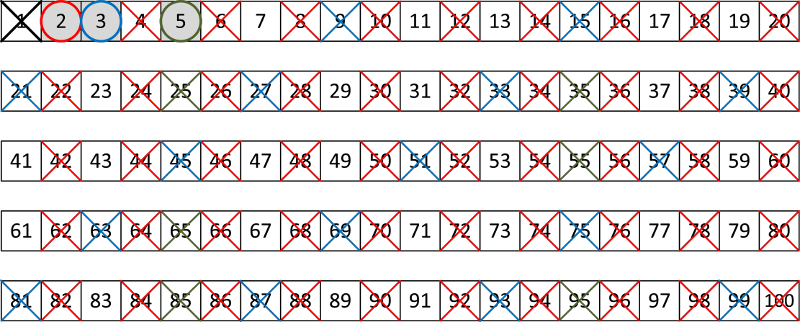
Korak 4

Sada izvršavamo isti postupak za broj 7.

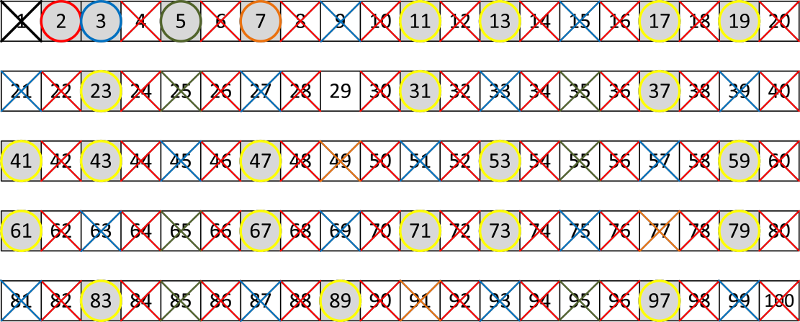
Primjećujemo da su u nizu ostali samo prosti brojevi i da se algoritam može zaustaviti nakon broja 7. Brojeve 8, 9 i 10 nećemo obrađivati jer nisu prosti, tj. već su izbačeni iz niza.

Implementacija

Implementacija algoritma Eratostenovo sito u Pythonu:

def nadji_proste_brojeve(n):
    prosti = set()
    slozeni = set()

    for i in range(2, n + 1):
        if i not in slozeni:
            prosti.add(i)
            for j in range(i * i, n + 1, i):
                slozeni.add(j)
    return prosti

print(nadji_proste_brojeve(100))

Izvor: boljiprogramer.com