Jedinični vektor

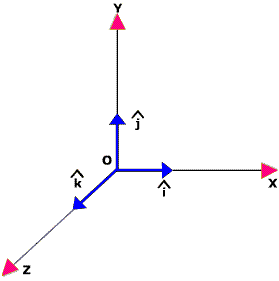
Jedinični vektor je vektor dužine 1. Možemo normalizovati svaki vektor u jedinični vektor.

Normalizacija vektora

Da bismo normalizovali vektor, podelimo svaku njegovu komponentu sa dužinom vektora:

jedinicni_vektor = (vektor.x / duzina, vektor.y / duzina, vektor.z / duzina)

Dužinu vektora računamo pomoću Pitagorine teoreme primenjene na 3D:

|v| = sqrt(x² + y² + z²)

Na primer, da normalizujemo vektor (3, 4), prvo računamo njegovu dužinu:

|v| = sqrt(3² + 4²) = sqrt(9 + 16) = sqrt(25) = 5

Potom delimo svaku komponentu dužinom vektora i dobijamo jedinični vektor:

v̂ = (3/5, 4/5)

Kod jediničnog vektora, ose se obično nazivaju:

i (normalizovana x osa)
j (normalizovana y osa)
k (normalizovana z osa)

Normalni vektori nemaju nikakve veze sa normalizacijom vektora. Vektori su normalni u odnosu na površinu kada su pod pravim uglom.

Upotreba u igrama

U igrama, kada radimo sa smerom (pored položaja i brzine), bitno je koristiti jedinične vektore.

Na primer, top uperen u smeru (1,0), dakle udesno, ispaljuje projektil pri brzini 20 m/s. Koja je vektorska brzina projektila? Jednostavno pomnožimo jedinični vektor i brzinu projektila da dobijemo vektorsku brzinu:

v = (1, 0) * 20 = (20, 0)

dakle projektil leti 20 m/s udesno.