Deo zbornika Učimo algoritme

Lista povezanosti

Lista povezanosti ili lista susjedstva (engl. adjacency list) je matrica u koju za svaki čvor u grafu zapisujemo njegove susjede. Za razliku od matrice susjedstva, lista susjeda može biti i grbava matrica (matrica kod koje veličine svih redova nisu jednake).

Na slici 2 vidimo vidimo listu susjeda koja odgovara grafu sa slike 1.

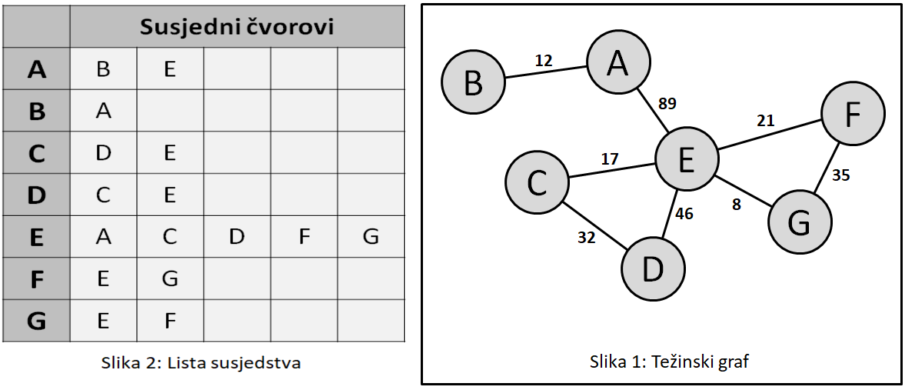
Kao što možemo vidjeti u prvom redu pišemo susjede čvora A, u drugom susjede čvora B itd. Da bi postigli efekat grbave matrice ne možemo koristiti obično dvodimenzionalno polje, nego su nam potrebni vektori.

Ukoliko, želimo da u listu susjeda zabilježimo i vrijednost grane između dva čvora moramo koristiti vektore. Tako bismo u LS[i][j].first pisali neki susjedni čvor čvora i, dok bi u LS[i][j].second pisali vrijednost grane između ta dva čvora (LS označava vektor vektora parova u koji ćemo smjestiti našu listu susjeda).

Prednost liste susjeda je to što možemo iterativno obilaziti postojeće grane, što kod matrice susjedstva nije moguće. Takođe, koristeći listu susjeda štedimo prostor (memoriju). Sa druge strane, mana liste susjeda je to što ne možemo u svakom trenutku provjeriti da li postoji grana između neka dva čvora.

Vežba

Pokušajmo riješiti sljedeći zadatak:

Unose se brojevi n i m, a zatim m puta po dva broja a i b, što znači da u grafu imamo jednosmjerni put od a do b. Potrebno je ispisati listu susjeda koja odgovara datom grafu (u i-tom redu treba da budu ispisani svi čvorovi do kojih postoji direktna grana iz čvora i).

#include <iostream>
#include <vector>
using namespace std;

int main()
{
    int n,m;
    cin>>n>>m;

    vector<int> Vi;
    vector<vector<int> > LS(n,Vi);

    int a,b;
    for (int i=0;i<m;i++)
    {
        cin>>a>>b;
        LS[a-1].push_back(b-1);
    }

    for (int i=0;i<n;i++)
    {
        cout<<i+1<<": ";
        for (int j=0;j<LS[i].size();j++)
            cout<<LS[i][j]+1<<' ';
        cout<<endl;
    }

    return 0;
}

Izvor: boljiprogramer.com