Loše strane rekurzije

Dobre strane rekurzije su (obično) čitljiv i kratak kod, jednostavan za razumevanje, analizu, dokazivanje korektnosti i održavanje. Ipak, rekurzivna rešenja imaju i mana.

Cena poziva

Prilikom svakog rekurzivnog poziva kreira se novi stek okvir i kopiraju se argumenti funkcije. Kada rekurzivnih poziva ima mnogo, ovo može biti veoma memorijski i vremenski zahtevno, te je poželjno rekurzivno rešenje zameniti iterativnim.

Suvišna izračunavanja

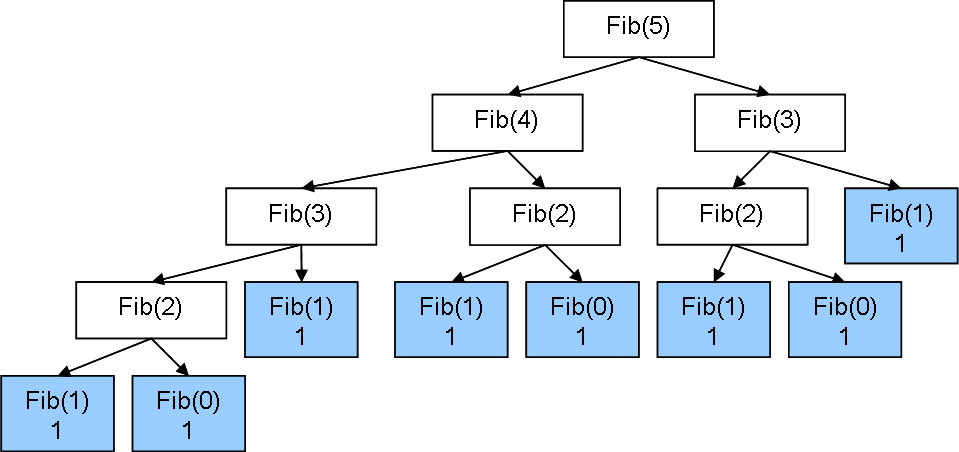
U nekim slučajevima prilikom razlaganja problema na manje potprobleme dolazi do preklapanja potproblema i do višestrukih rekurzivnih poziva za iste potprobleme.

Razmotrimo, na primer, izvršavanje navedene funkcije koja izračunava elemente Fibonačijevog niza za n = 5. U okviru tog izvršavanja, funkcija fib je 3 puta pozvana za n = 0, 5 puta za n = 1, itd. Naravno, na primer, poziv fib(1) je svaki put izvršavan iznova i nije korišćena vrednost koju je vratio prethodni takav poziv. Zbog ovoga, izvršava se mnogo suvišnih izračunavanja i količina takvih izračunavanja u ovom primeru raste.

Rešenje 1: Memoizacija

Kako bi se izbegla suvišna izračunavanja moguće je koristiti tehniku memoizacije, koja podrazumeva da se u posebnoj strukturi podataka čuvaju svi rezultati već završenih rekurzivnih poziva. Pri svakom ulasku u funkciju konsultuje se ova struktura i, ako je rezultat već poznat, vraća se prethodno izračunat rezultat.

unsigned memo[MAX_FIB];
unsigned fib(unsigned n) {
    if (memo[n]) return memo[n];
    if (n == 0 || n == 1)
        return memo[n] = n;
    else
        return memo[n] = fib(n-1) + fib(n-2);
}

Rešenje 2: Iterativna funkcija

Gore navedena funkcija fib može se zameniti iterativnom funkcijom koja od početnih elemenata niza postepeno sintetiše sve dalje i dalje elemente niza. Primetimo da za izračunavanje n-tog elementa niza nije neophodno pamtiti sve elemente niza do indeksa n već samo dva prethodna:

int fib(int n) {
    int i, fpp, fp;

    if (n == 0 || n == 1)
        return n;

    fpp = 0;
    fp = 1;

    for(i = 2; i <= n; i++) {
        int f = fpp + fp;
        fpp = fp;
        fp = f;
    }

    return fp;
}

Izvor: Predrag Janičić i Filip Marić, PROGRAMIRANJE 2, Osnove programiranja kroz programski jezik C, Beograd, 2017.