Deo zbornika Teorija razvoja igara

Matrica inverzije

Matrica inverzije se koristi za poništavanje efekta određene transformacije, kao što je rotacija, skaliranje, translacija itd. Matrica koja poništava efekt originalne matrice A naziva se A⁻¹ i mora zadovoljiti:

A * A⁻¹ = I (identična matrica)

Sleci nekoliko primera matrica inverzije za osnovne transformacije.

Inverzija rotacije

2D rotaciona matrica je:

R(θ) = [cos(θ), -sin(θ)]
       [sin(θ), cos(θ)]

Inverzija rotacije je rotacija u suprotnom smeru, što znači zamenu predznaka u matrici:

R⁻¹(θ) = [cos(θ), sin(θ)]
         [-sin(θ), cos(θ)]

Inverzija skaliranja

2D matrica skaliranja je:

S(kx, ky) = [kx, 0]
            [0, ky]

Inverzija ove matrice je recipročna vrednost skaliranja:

S⁻¹(kx, ky) = [1/kx, 0]
              [0, 1/ky]

Inverzija 3D skaliranja

Matrica za 3D skaliranje je:

S(kx, ky, kz) = [kx, 0, 0]
                [0, ky, 0]
                [0, 0, kz]

Inverzija ove matrice je:

S⁻¹(kx, ky, kz) = [1/kx, 0, 0]
                  [0, 1/ky, 0]
                  [0, 0, 1/kz]

Inverzija translacije

2D translaciona matrica je:

T(dx, dy) = [1, 0, dx]
            [0, 1, dy]
            [0, 0, 1]

Inverzija translacije je translacija u suprotnom smeru:

T⁻¹(dx, dy) = [1, 0, -dx]
              [0, 1, -dy]
              [0, 0, 1]

Inverzija odraza

Na primer, za 2D odraz preko x ose, matrica izgleda ovako:

F = [1, 0]
    [0, -1]

Inverzija odraza je ista matrica jer dvostruki odraz daje originalnu sliku, što znači da je F⁻¹ = F.

Zakon inverzije

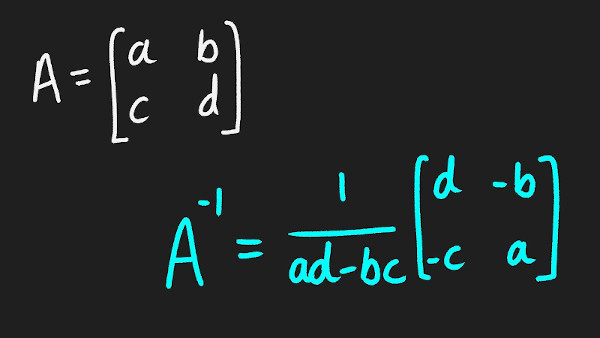
Generalno, da bi se našla inverzna matrica za transformaciju, koristi se formula za inverziju matrica koja zavisi od dimenzionalnosti. Za matricu A dimenzije 2x2, inverzija se može izračunati pomoću sledeće formule:

A⁻¹ = 1/det(A) * [d, -b]
                 [-c, a]

Gde su

• a, b, c, d: elementi matrice
• det(A) = ad - bc: determinanta matrice

Za veće matrice (3x3 i više), proces je složeniji i zahteva korišćenje metoda kao što su Gauss-Jordan eliminacija ili korišćenje kofaktora i determinanti.