Deo zbornika Teorija razvoja igara

Matrica rotacije

Matrica rotacije služi za okretanje predmeta ili celokupnog prostora oko određene tačke ili ose. Podrazumevano, matrica rotacije rotira objekat u odnosu na ishodište.

U dve dimenzije postoji samo jedna moguća osa rotacije, pa nam je potreban samo ugao. U 3D je dosta složenije: postoje tri primarne ose rotacije, a telo može rotirati i oko bilo koje proizvoljne ose.

2D rotacija

2D rotacija oko ishodišta u smeru kazaljke:

cos(θ), -sin(θ)
sin(θ),  cos(θ)

2D rotacija oko ishodišta u smeru suprotnom od kazaljke:

 cos(θ) sin(θ)
-sin(θ) cos(θ)

Posebni slučajevi

Obzirom da je cos(90) = 0, a sin(90) = 1, postoje posebne rotacije koje samo obrću unete vrednosti:

rotacija 90°  = (x, y) => (-y, x)
rotacija 180° = (x, y) => (-x, -y)
rotacija 270° = (x, y) => (y, -x)

Objašnjenje: Kada zamenimo vrednosti sin i cos u matrici rotacije dobijemo:

R(90°) = 0, -1
         1,  0

Množenje ove matrice sa (x, y) daje (-y, x).

3D rotacija

Rotacija oko x ose za ugao θ:

1,      0,       0
0, cos(θ), -sin(θ)
0, sin(θ),  cos(θ)

Rotacija oko y ose za ugao θ:

cos(θ),  0, sin(θ)
0,       1,      0
-sin(θ), 0, cos(θ)

Rotacija oko z ose za ugao θ:

cos(θ), -sin(θ), 0
sin(θ),  cos(θ), 0
0,       0,      1

Homogeni zapis

Matrica rotacije oko x-ose:

  0       0    0  
 cosθ  -sinθ   0  
 sinθ   cosθ   0  
  0       0    1

Matrica rotacije oko y-ose:

cosθ   0   sinθ   0  
0      1      0    0  
-sinθ  0   cosθ   0  
0      0      0    1

Matrica rotacije oko z-ose:

cosθ  -sinθ   0    0  
sinθ   cosθ   0    0  
0      0      1    0  
0      0      0    1

Primer: Tarzan

Recimo da igrač treba da se ljulja na lijani. Možemo primeniti rotaciju oko tačke gde je lijana pričvršćena. Dakle, treba izračunati ugao između igrača i centra rotacije, povećavati ga i sledstveno ažurirati poziciju igrača.

Ugao između igrača i centra rotacije računamo pomoću atan2(). Nakon što povećamo ugao, možemo izračunati nove x i y koordinate sa sin i cos:

ugao = atan2(y, x)
duzina = sqrt(x * x + y * y)
ugao += 1
nov_x = duzina * cos(ugao)
nov_y = duzina * sin(ugao)

Pošto konvertujemo iz kartezijanskih koordinata u polarne, i ponovo nazad, možemo izgubiti preciznost. Bolji način je matrica rotacija, koja omogućuje rotiranje bez međukoraka:

nov_x = x * cos(ugao) - y * sin(ugao)
nov_y = x * sin(ugao) + y * cos(ugao)

Optimizacija: razumno je unapred izračunati cos i sin, jer nam treba dvaput.

Primer: Svemirski brod

Recimo da pravimo igru Asteroidi, i imamo jednostavan 2D svemirski brod koji se može slobodno rotirati. Model broda izgleda ovako:

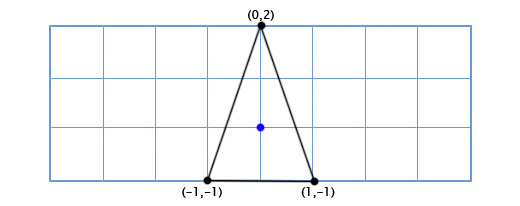
Kako crtati brod rotiran za proizvoljan ugao, na primer za 49 stepeni u smeru suprotnom od kazaljke? Pomoću trigonometrije možemo napraviti funkciju koja prima tačku i ugao, te vraća rotiranu tačku:

vec2 rotate(vec2 point, float angle){
   vec2 rotated_point;
   rotated_point.x = point.x * cos(angle) - point.y * sin(angle);
   rotated_point.y = point.x * sin(angle) + point.y * cos(angle);
   return rotated_point;
}

Primenom funkcije na tri tačke broda dobijamo sledeći oblik:

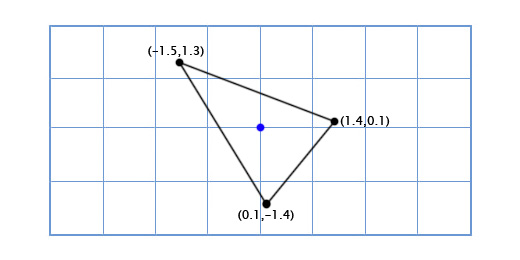
Operacije kosinusa i sinusa su prilično spore, ali smo ih radili samo na tri tačke. Međutim, sada odlučujemo da nadogradimo brod da izgleda ovako:

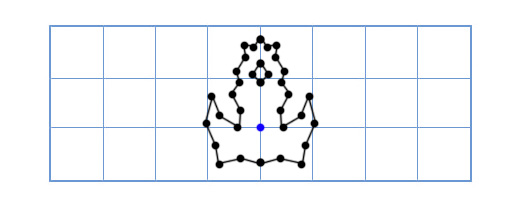
Sada je stara funkcija prespora! Elegantno rešenje bi bilo da umesto svake tačke ponaosob rotiramo samo x i y osu modela.

Objašnjenje: Pozicija (3,2) znači 3 * x osa plus 2 * y osa. Podrazumevano, x osa = (1,0), y osa = (0,1), pa dobijamo 3(1,0) + 2(0,1). Međutim, ako rotiramo ose, lako ćemo izračunati svaku tačku koja zavisi od njih.

rotiranje (1,0) za 49 stepeni = (0,66, 0,75) // nova x osa
rotiranje (0,1) za 49 stepeni = (-0,75, 0,66) // nova y osa

Za modifikovane ose (a,b) i (c,d), novu tačku (x,y) možemo naći pomoću ovog izraza:

x(a,b) + y(c,d)