Oduzimanje vektora

Vektore oduzimamo jedan od drugog na sledeći način:

prvo obrnemo pravac vektora koji želimo da oduzmemo (npr. b)
zatim ih sabiramo

Oduzimanje vektora a - b isto je što i sabiranje a i –b:

a - b = a + (-b)

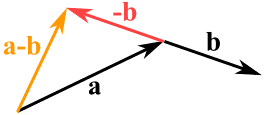
vector-subtract

Procedura oduzimanja vektora je sledeća:

a - b = [(a.x - b.x), (a.y - b.y), (a.z - b.z)]

Ciljanje protivnika u igrama

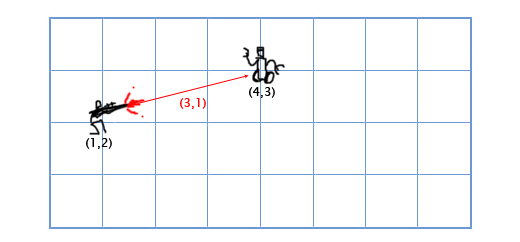
U igrama, oduzimanje vektora je korisno za dobijanje vektora koji vodi od jedne pozicije do druge. Da bismo ga izračunali, oduzimamo početnu tačku od krajnje tačke.

Na primer, igrač sa laserskom puškom stoji na poziciji (1,2), a neprijateljski robot na (4,3). Da dobijemo vektor kojim laser pogađa robota, oduzimamo poziciju igrača od pozicije robota:

(4, 3) - (1, 2) = (4-1, 3-2) = (3, 1)

Implementacija prateće rakete

U igri nam ponekad zatreba da igrač može ispaljivati prateće rakete. Da bismo to implementirali, prvo računamo vektor razdaljine, tako što oduzmemo položaj rakete od položaja cilja:

razdaljina.x = target.x - raketa.x
razdaljina.y = target.y - raketa.y

Sada možemo izračunati ugao pod kojim raketa treba da ide, pomoću trigonometrijske funkcije atan2():

ugao = atan2(razdaljina.y, razdaljina.x)

Ukoliko želimo da raketa prati cilj i nakon lansiranja, potrebno je povremeno ažurirati ovaj ugao.