Parabola

parabola

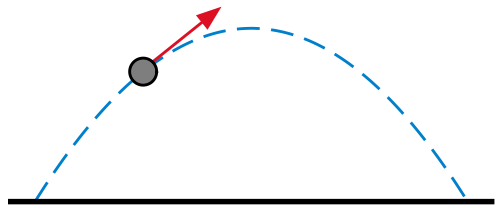
Svaki projektil prati paraboličnu putanju. Parabola je stručni naziv za luk. Ukoliko u igri ne koristimo fizičku simulaciju, pomoću jednačine parabole možemo simulirati let projektila.

Jednačina parabole

Parabolu sa vertikalnom osom simetrije opisuje sledeća jednačina:

y = a * (x – h)² + k

gde je:

y: vertikalna vrednost za dati x
x: zadata horizontalna vrednost
(h, k): tačka vrha
a: koeficijent orijentacije i nagiba parabole
- a = -1: parabola je vrhom gore
- a = 1: parabola je vrhom dole
- a = (-)2: parabola uža, a = (-)0.5 parabola šira

parabola

Primer: Putanja strele

Igrač gađa strelom koja se kreće lučno dok pada pod uticajem gravitacije.

function getParabolaY(x, a, h, k) {
    return a * Math.pow(x - h, 2) + k
}

const a = -0.1 // širina parabole
const h = 5
const k = 3

for (let x = 0; x <= 10; x++) {
    console.log(`x=${x}, y=${getParabolaY(x, a, h, k)}`)
}

Primer: Skakanje lika

Lik u igri skače lučno dok se spušta nazad na platformu.

function getParabolaY(x, a, h, k) {
    return a * Math.pow(x - h, 2) + k
}

const a = -2   // oblik parabole
const h = 1
const k = 5

for (let x = 0; x <= 2; x += 0.1) {
    console.log(`x=${x.toFixed(1)}, y=${getParabolaY(x, a, h, k).toFixed(2)}`)
}

Primer: Lučno kretanje kamere

Kamera lučno prelazi iz jedne tačke u drugu, npr. kod prelaska nivoa.

function getParabolaY(x, a, h, k) {
    return a * Math.pow(x - h, 2) + k
}

const a = 0.5  // oblik parabole
const h = 10
const k = 5

for (let x = 0; x <= 20; x++) {
    console.log(`x=${x}, y=${getParabolaY(x, a, h, k)}`)
}