Perspektivna projekcija

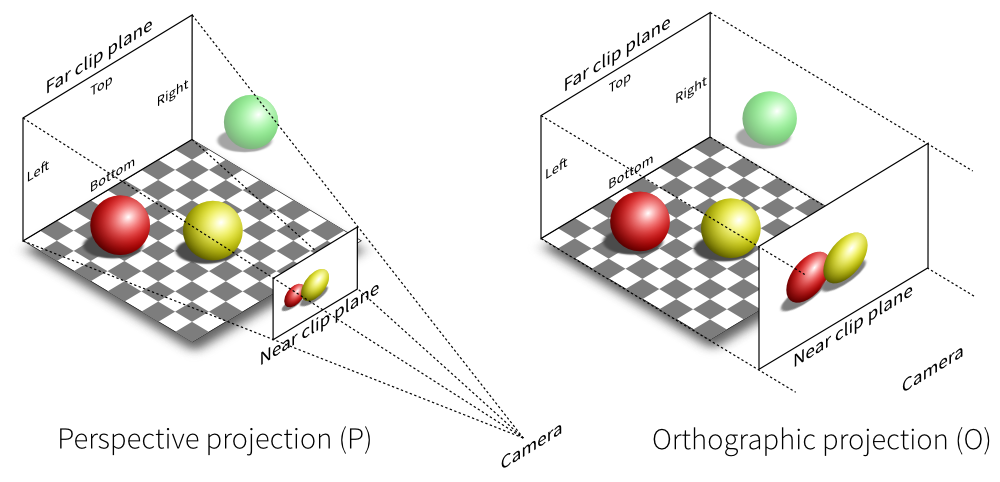
perspektiva

3D svet se najbolje predstavlja projekcijom na 2D ravan uz primenu perspektive. Što je predmet dalje od kamere to deluje manje na slici, kao što i oči prirodno vide.

Oblik 3D perspektivne projekcije se naziva frustum, odnosno piramida čiji je vrh odsečen pomoću ravni koja je paralelna njenoj osnovi.

Za razliku od ortogonalne, perspektivna projekcija se oslanja na koncept fokalne tačke.

2D projekcija

Da bismo razumeli 3D projekciju, razmotrimo 2D projekciju:

P je tačka koju projektujemo
zelena linija je projekcijska ravan, na odstojanju Ez od oka (0,0,0)
R je projektovana tačka
imamo dva slična pravougaona trougla: manji (E, R i Ez) i veći (E, P i Pz)

Da bismo našli položaj R, koristimo formulu:

R = P * (Ez / Pz)

Ova formula jednako radi u 2D i 3D. Perspektivna projekcija je samo primena ove formule na svaki vrh.

Primer: projekcija kocke

Implementacija perspektivna projekcije u kodu:

const canvas = document.getElementById('canvas')
const ctx = canvas.getContext('2d')

// x, y, z
const vrhovi = [
  [-1, -1, -1], [1, -1, -1], [1, 1, -1], [-1, 1, -1], // zadnja strana
  [-1, -1, 1], [1, -1, 1], [1, 1, 1], [-1, 1, 1]      // prednja strana
]

const ivice = [
  [0, 1], [1, 2], [2, 3], [3, 0], // zadnja strana
  [4, 5], [5, 6], [6, 7], [7, 4], // prednja strana
  [0, 4], [1, 5], [2, 6], [3, 7]  // veze između
]

function projektuj([x, y, z]) {
  const skalar = 200 / (z + 4)
  return [canvas.width / 2 + x * skalar, canvas.height / 2 - y * skalar]
}

function crtaj() {
  ctx.clearRect(0, 0, canvas.width, canvas.height)
  ivice.forEach(([start, end]) => {
    const [x1, y1] = projektuj(vrhovi[start])
    const [x2, y2] = projektuj(vrhovi[end])
    ctx.beginPath()
    ctx.moveTo(x1, y1)
    ctx.lineTo(x2, y2)
    ctx.stroke()
  })
}

void function animiraj() {
  vrhovi.forEach(v => {
    v[0] = v[0] * Math.cos(0.01) - v[2] * Math.sin(0.01)
    v[2] = v[0] * Math.sin(0.01) + v[2] * Math.cos(0.01)
  })
  crtaj()
  requestAnimationFrame(animiraj)
}()

Perspektivna projekcija pomera vrhove prema oku, na osnovu njihovog položaja. Vrhovi koji su dalje na z osi pomeraju se manje nego oni koji su bliže. Formula za skaliranje:

skalar = 200 / (z + 4) 

određuje koliki će predmet biti na ekranu, na osnovu njegove dubine (z). 200 je osnovni skalar. Kako z raste (predmet je dalje), veličina se smanjuje. Dodavanje + 4 sprečava da predmet postane previše mali ili beskonačno veliki kada je blizu posmatrača.

Primer: projekcija ravni

Rotiramo ravan u 3D prostoru tako što menjamo uglove rotacije oko X i Y osa. Rotacija se obavlja pomoću trigonometrijskih funkcija, a zatim se tačke projektuju na 2D ekran kako bi izgledale kao da su u prostoru.

const canvas = document.getElementById('canvas1')
const ctx = canvas.getContext('2d')

const d = 500
let angleX = 0, angleY = 0

const points = [
  { x: -200, y: 0, z: -200 },
  { x: 200, y: 0, z: -200 },
  { x: 200, y: 0, z: 200 },
  { x: -200, y: 0, z: 200 }
]

const rotiraj = (point, angleX, angleY) => ({
  x: point.x * Math.cos(angleY) + point.z * Math.sin(angleY),
  y: point.y * Math.cos(angleX) - point.z * Math.sin(angleX),
  z: point.x * -Math.sin(angleY) + point.z * Math.cos(angleY) + point.y * Math.sin(angleX)
})

const projektuj = point => ({
  x: point.x * d / (point.z + d) + canvas.width / 2,
  y: point.y * d / (point.z + d) + canvas.height / 2
})

function crtaj() {
  ctx.clearRect(0, 0, canvas.width, canvas.height)

  const rotatedPoints = points.map(p => rotiraj(p, angleX, angleY))
  const projectedPoints = rotatedPoints.map(p => projektuj(p))

  ctx.beginPath()
  projectedPoints.forEach((p, i) =>
    i === 0 ? ctx.moveTo(p.x, p.y) : ctx.lineTo(p.x, p.y)
  )
  ctx.closePath()
  ctx.stroke()

  ctx.fillStyle = 'rgb(0, 200, 0)'
  ctx.fill()
}

function animiraj() {
  angleX += 0.005
  angleY += 0.005
  crtaj()
}

setInterval(animiraj, 1000 / 60)  // 60 FPS

Primer: projekcija sfere

const canvas = document.getElementById('canvas2')
const ctx = canvas.getContext('2d')

const radius = 150
const planetSpeed = 0.005
let angle = 0

const centerX = canvas.width / 2
const centerY = canvas.height / 2
const perspective = 300

function drawPlanet() {
  ctx.clearRect(0, 0, canvas.width, canvas.height)

  for (let phi = 0; phi < Math.PI; phi += 0.1)
    for (let theta = 0; theta < 2 * Math.PI; theta += 0.1) {
      const x3D = radius * Math.sin(phi) * Math.cos(theta)
      const y3D = radius * Math.sin(phi) * Math.sin(theta)
      const z3D = radius * Math.cos(phi)

      const xRot = x3D * Math.cos(angle) - z3D * Math.sin(angle)
      const zRot = x3D * Math.sin(angle) + z3D * Math.cos(angle)

      const scale = perspective / (perspective + zRot)
      const x2D = centerX + xRot * scale
      const y2D = centerY + y3D * scale

      ctx.beginPath()
      ctx.arc(x2D, y2D, 2, 0, 2 * Math.PI)
      ctx.fillStyle = 'blue'
      ctx.fill()
    }

}

function animate() {
  requestAnimationFrame(animate)
  angle += planetSpeed
  drawPlanet()
}

animate()

Primer: projekcija tačaka u ravni

U ovom primeru, tačke se rotiraju u 3D prostoru, preslikavaju u 2D koristeći perspektivu i crtaju na platnu.

const canvas = document.getElementById('canvas3')
const ctx = canvas.getContext('2d')

const fov = 500

const pixels = []
for (let x = -100; x <= 100; x += 10)
  for (let z = -100; z <= 100; z += 10)
    pixels.push({ x, y: 40, z })

let angle = 0

function render() {
  ctx.clearRect(0, 0, canvas.width, canvas.height)
  pixels.forEach(p => {
    const zRot = Math.cos(angle) * p.z - Math.sin(angle) * p.x
    const xRot = Math.sin(angle) * p.z + Math.cos(angle) * p.x
    const scale = fov / (fov + zRot)
    const x2d = xRot * scale + canvas.width / 2
    const y2d = p.y * scale + canvas.height / 2
    ctx.fillRect(x2d, y2d, 2, 2)
  })
  angle += 0.005
  requestAnimationFrame(render)
}

render()

Primer: projekcija tačaka u kocki

const canvas = document.getElementById('canvas4')
const ctx = canvas.getContext('2d')

const w2 = canvas.width / 2, h2 = canvas.height / 2
const { cos } = Math, { sin } = Math, pi = Math.PI

let skalar = 200
let ugao1 = 0
let ugao2 = 0

function project(x, y, z) {
  const x1 = x * cos(ugao1) + z * sin(ugao1)
  const z1 = -x * sin(ugao1) + z * cos(ugao1)
  const x2 = x1
  const y2 = y * cos(ugao2) + z1 * sin(ugao2)
  const z2 = -y * sin(ugao2) + z1 * cos(ugao2) + 300
  const d = 500 / z2
  const x3 = (skalar / z2) * x2 + w2
  const y3 = (skalar / z2) * y2 + h2
  ctx.beginPath()
  ctx.arc(x3, y3, d, 0, 2 * pi)
  ctx.fill()
}

function loop() {
  ctx.clearRect(0, 0, canvas.width, canvas.height)
  const x = 100, y = 100, z = 100

  for (let i = 0; i < 5; i++)
    for (let j = 0; j < 5; j++) {
      const xj = 0.5 * j * x - 100
      const yi = 0.5 * i * y - 100
      const zj = 0.5 * j * z - 100
      const zi = 0.5 * i * z - 100
      project(xj, yi, -z)
      project(xj, yi, z)
      project(x, yi, zj)
      project(-x, yi, zj)
      project(xj, y, zi)
      project(xj, -y, zi)
    }

  ugao1 += 0.02
  ugao2 += 0.03
  window.requestAnimationFrame(loop)
}

loop()

Literatura

Etay Meiri, Perspective projection