Deo zbornika Učimo algoritme
Pretraga u dubinu
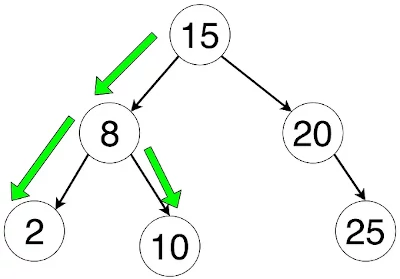
Pretraga u dubinu (depth-first search) se može koristiti kad je potrebno nizom koraka stići od polazne pozicije do završne. Traženje puta u lavirintu je verovatno najpoznatiji primer primene ovog algoritma. Drugi primeri su Lojdova slagalica od 15 brojeva i problem osam dama.
Izlaz iz lavirinta

Kako biste tražili put kroz lavirint?
Ideja koja je ovde opisana verovatno vam je već poznata: ostavljate iza sebe trag (mrvice, kamenčiće, nit konca…) i napredujete dok god možete. Kada dođete do mesta sa kojeg se ne može dalje napredovati, vraćate se unazad tragom do najbližeg mesta sa kojeg možete krenuti novom putanjom i nastavljate njom. Ovako postupate dok ne nađete izlaz, ili dok ne istražite sve putanje (što bi značilo da izlaz ne postoji).
Ovo je u osnovi algoritam pretrage najpre u dubinu. Pretraga se zove najpre u dubinu jer prvo idete dublje u lavirint dokle god možete, a vraćate se samo ako ne možete dalje u dubinu. Osim pretrage u dubinu, mogli bismo na primer, prvo da označimo sva mesta na koja možemo da stignemo u jednom koraku, zatim ona na koja možemo da stignemo u dva koraka i tako dalje, što se zove pretrage najpre u širinu.
Razmotrimo još jedno pitanje: da li pri vraćanju tragom treba trag uklanjati ili ostavljati? Ako bismo uklanjali trag, moglo bi se dogoditi da ista polja posećujemo veliki broj puta iz raznih pravaca. Ako bismo pak ostavljali trag i posle vraćanja, bilo bi komplikovanije prikazati putanju od polazne do tekuće pozicije i razlikovati je od delova lavirinta kojima smo išli i vratili se (slepi krakovi). Kako obe odluke imaju dobrih i loših strana, u opštem slučaju je najbolje da koristimo dve vrste traga, jedan kada napredujemo, a drugi kada se vraćamo. Tako uvek imamo jasno označenu putanju od polazne do tekuće pozicije (koja u slučaju nailaska na izlaz postaje rešenje), a takođe i garanciju da ćemo svako polje lavirinta posetiti najviše jedanput.
Primer u pseudokodu
Lavirint je predstavljen matricom a. Funkcija Seek kojom tražimo izlaz prima koordinate tekućeg polja kao argumente. Pretpostavljamo da su sam lavirint i njegove dimenzije rowCnt i colCnt dostupni funkciji. Funkcija vraća vrednost koja govori da li je put pronađen. Algoritam traženja puta mogao bi se ovako zapisati:
Seek(i, j)
if (i < 1) or (j < 1) or (i > rowCnt) or (j > colCnt)
return false;
if (a[i][j] = kExit)
PrintMatrix();
return true;
if (a[i][j] != kPass)
return false;
a[i][j] = kSearching;
bool found = Seek(i-1, j) or Seek(i, j-1) or Seek(i+1, j) or Seek(i, j+1);
a[i][j] = kSearched;
return found;
Trajanje pretrage je u najgorem slučaju srazmerno veličini prostora pretrage. Pretraga zahteva prostor srazmeran najvećoj dostignutoj dubini, što u najgorem slučaju može biti isto što i veličina prostora pretrage. U rekurzivnoj implementaciji, koja je jednostavnija, ta memorija se koristi implicitno za stek rekurzivnih poziva. U nerekurzivnoj implementaciji bilo bi neophodno pamtiti niz polja koja su posećena, a kroz koja pretraga još uvek traje (polja označena vrednošću kSearching).
Primer u JS-U
Ovaj kod pravi graf, dodaje čvorove i ivice, i izvodi DFS pretragu od čvora 1:
class Graph {
constructor() {
this.adjList = new Map()
}
addVertex(vertex) {
this.adjList.set(vertex, [])
}
addEdge(v1, v2) {
this.adjList.get(v1).push(v2)
this.adjList.get(v2).push(v1)
}
dfs(start) {
const visited = new Set()
const result = []
const dfsHelper = (vertex) => {
if (!visited.has(vertex)) {
visited.add(vertex)
result.push(vertex)
this.adjList.get(vertex).forEach(neighbor => dfsHelper(neighbor))
}
}
dfsHelper(start)
return result
}
}
// upotreba
const graph = new Graph()
graph.addVertex(1)
graph.addVertex(2)
graph.addVertex(3)
graph.addVertex(4)
graph.addEdge(1, 2)
graph.addEdge(1, 3)
graph.addEdge(2, 4)
console.log(graph.dfs(1))
Lojdova slagalica

U slučaju Lojdove slagalice, početna pozicija je nasumična, završna je ona na kojoj su brojevi poređani po veličini (kao na slici), a potez se izvršava tako što prazno polje zameni mesto sa nekim njemu susednim poljem. Broj pozicija u ovoj igri je toliko veliki da njihova kompletna pretraga može trajati vrlo dugo. Da ne bismo prolazili ceo prostor pretrage, poželjno je na neki inteligentan način birati sledeći potez.
Postoji niz poboljšanja pretrage u dubinu i upravo ova slagalica je odličan primer kako se pretraga može ubrzati usmeravanjem i ograničavanjem.
Izvori
- Petlja.org: Pretraga “najpre u dubinu” i “najpre u širinu”