Deo zbornika Učimo algoritme
Pretraga u širinu
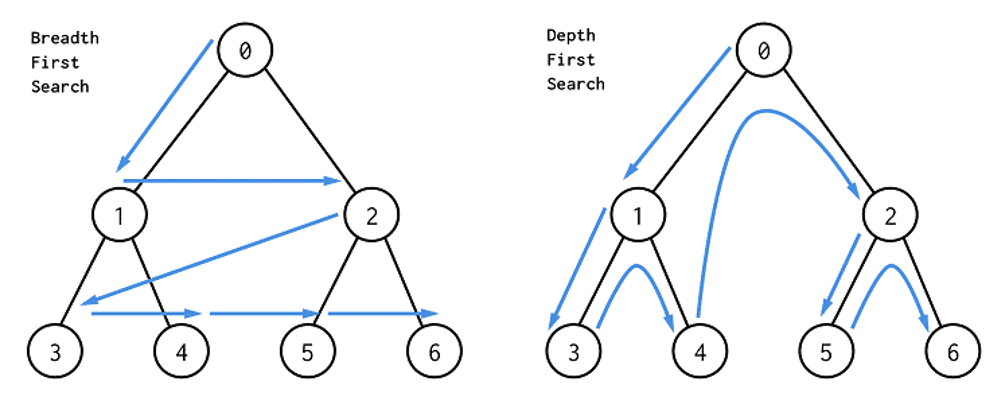
Pretraga u širinu (breadth first search, BFS) je algoritam za pretragu stabala i grafova, gde krećemo od početnog čvora i prelazimo sve njegove susede pre nego što pređemo na sledeći nivo. Tako se osigurava da prvo pretražimo trenutni nivo pre nego što nastavimo dublje.
Pretraga u širinu se od pretrage u dubinu razlikuje po redosledu obilaska. Ovom pretragom se prvo pronalaze sve pozicije dostupne posle jednog poteza, zatim sve dostupne posle dva poteza, itd.
Algoritam pretrage u širinu koristi strukturu podataka koja se naziva red. Objekti mogu da se dodaju na kraj reda, a objekat koji je na početku reda može da se uzme i upotrebi. U slučaju lavirinta, objekti predstavljaju pozicije iz prostora pretrage, a to su dostignuta polja.
Prednosti i mane
Prednost pretrage u širinu je što se prva poseta svake nove pozicije uvek postiže u najmanjem mogućem broju koraka. Zahvaljujući tome, rešenja otkrivena pretragom u širinu su uvek optimalna po broju koraka.
Sa druge strane, radi pretrage u širinu potrebno je organizovati pamćenje posećenih pozicija, da bi se pretraga mogla nastaviti iz njih.
Primer u pseudokodu: Izlaz iz lavirinta
Matricom a je dat lavirint i polazno polje u njemu. Zadatak je da se za svako polje lavirinta odredi najmanji broj koraka koji potreban da se do tog polja stigne.
Stavljamo u red koordinate polja koja su susedna posećenim, tako da ona čekaju da budu posećena. Za svako polje u pomoćnoj matrici m pamtimo broj koraka potreban za stizanje do njega.
MinMoves(xstart, ystart)
dirx[4] = {1, -1, 0, 0}; // Ovaj niz, zajedno sa sledecim zadaje 4 moguca smera kretanja
diry[4] = {0, 0, 1, -1};
for r = 1 to rowCnt
for c = 1 to colCnt
m[r][c] = infinity;
queue<Square> q;
q.push(Square(xstart, ystart));
m[ystart][xstart]=0;
while (!q.empty())
x = q.front().x;
y = q.front().y;
q.pop();
for dir = 1 to 4
xx = x + dirx[dir];
yy = y + diry[dir];
if (xx > 0 && yy > 0 && xx <= rowCnt && yy <= colCnt &&
m[yy][xx] == infinity && a[yy][xx] != kWall)
m[yy][xx] = m[y][x] + 1;
q.push(Square(xx, yy));
// Ispisivanje izracunate matrice
for r = 1 to rowCnt
for c = 1 to colCnt
if (m[r][c] == infinity)
Write('.');
else
Write(m[r][c]);
WriteLine();
Prilikom pretrage u širinu želimo da dodamo u red samo susede tekućeg polja koji još nisu posećeni. Posećena polja se prepoznaju po tome što imaju upisan potreban broj poteza.
Vreme rada i zauzeće memorije su u najgorem slučaju srazmerni veličini prostora pretrage.
Primer u JS-U
Jednostavna implementacija pretrage u širinu u JavaScript-u:
function bfsMaze(maze, start, end) {
const directions = [
[0, 1], [1, 0], [0, -1], [-1, 0] // desno, dole, levo, gore
]
const rows = maze.length
const cols = maze[0].length
const queue = [[start, [start]]]
const visited = new Set()
visited.add(start.toString())
while (queue.length > 0) {
const [[x, y], path] = queue.shift()
if (x === end[0] && y === end[1]) return path
for (const [dx, dy] of directions) {
const nx = x + dx, ny = y + dy
if (
nx >= 0 && ny >= 0 && nx < rows && ny < cols &&
maze[nx][ny] === 0 && !visited.has([nx, ny].toString())
) {
queue.push([[nx, ny], [...path, [nx, ny]]])
visited.add([nx, ny].toString())
}
}
}
return null
}
// upotreba
const maze = [
[0, 1, 0, 0],
[0, 1, 0, 1],
[0, 0, 0, 1],
[1, 1, 0, 0]
]
const start = [0, 0], end = [3, 3]
console.log(bfsMaze(maze, start, end)) // koraci do cilja
Izvori
- Petlja.org: Pretraga “najpre u dubinu” i “najpre u širinu”