Deo zbornika Teorija razvoja igara

Primena trigonometrije

Trigonometrijske funkcije su posebno bitne za razvoj igara. Koriste se za računanje ugla i rastojanja ka nekom predmetu, simulaciju fizike, modelovanje kružnog kretanja, talasa i drugih periodičnih pojava.

Računanje visina drveta

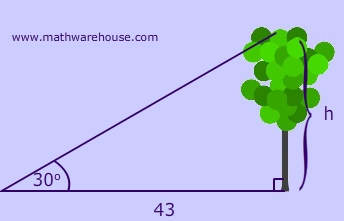
Bez merenja visine drveta, možemo je izračunati pomoću trigonometrije. Dovoljno je da izaberemo neku tačku, odokativno utvrdimo ugao ka vrhu drveta, i izmerimo rastojanje do podnožja.

Ovde nam može pomoći tangens funkcija:

tan(α) = visina / rastojanje

Pošto je visina nepoznata, menjamo mesta u jednačini:

visina = rastojanje × tan(α)

Na isti način možemo saznati visinu zgrade i bilo kog drugog objekta:

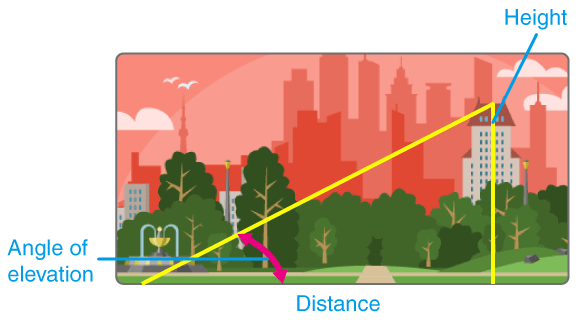
Računanje širine reke

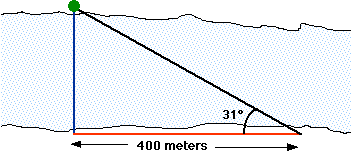
Po istom principu može izračunati širinu reke, ne prelazeći je. Koraci su sledeći:

• izaberemo neki predmet na drugoj strani reke kao orijentir
• pomerimo se nekoliko metara ulevo ili udesno, i izmerimo rastojanje
• sa novog položaja odredimo ugao kao orijentiru
• primenimo formulu širina = rastojanje × tan(ugla)

Računanje veličine Zemlje

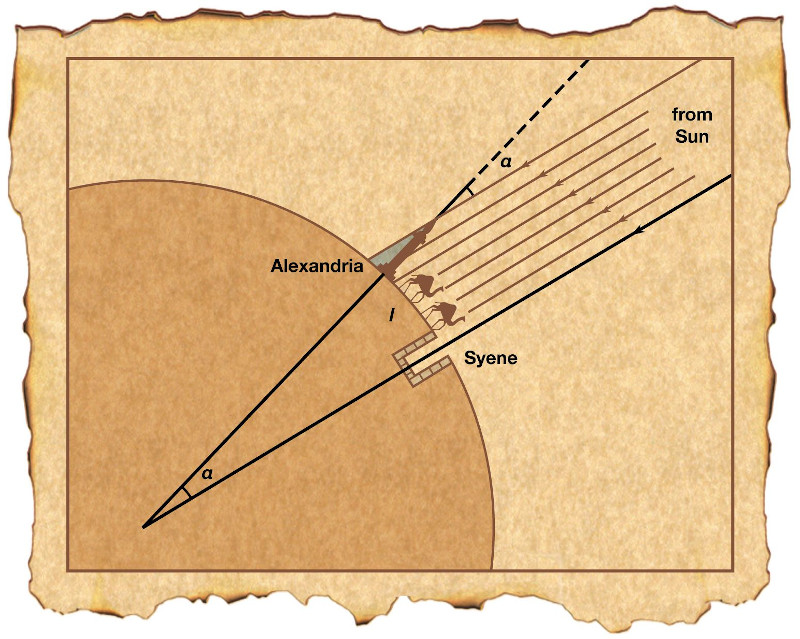
Starogrčki naučnik Eratosten (3. vek p.n.e.) je izračunao obim i poluprečnik planete Zemlje pomoću trigonometrije.

On je znao da u podne letnje dugodnevnice zraci Sunca obasjavaju dno bunara u Sijeni. U isto vreme, izmerio je da u Aleksandriji sunčevi zraci padaju pod uglom od 7°12’, što je 1/50 kruga. Znajući da je rastojanje između tih mesta 805 kilometara, izračunao je obim zemlje sa izuzetnom preciznošću (99,81%).

Izmerivši obim, pomoću formule kruga dobio je i poluprečnik naše planete.

Primer: Crtanje kruga

Pomoću trigonometrijskih funkcija možemo nacrtati krug:

const canvas = document.getElementById('canvas')
const ctx = canvas.getContext('2d')

const length = 50
let angle = 0.0

while (angle < 2 * Math.PI) {
  const x = length * Math.cos(angle)
  const y = length * Math.sin(angle)
  ctx.fillRect(x + canvas.width / 2, y + canvas.height / 2, 1, 1)
  angle += 0.1
}

Primer: Kruženje nebeskih tela

Možemo koristiti sinus i kosinus za animaciju orbite planete:

const canvas = document.getElementById('canvas2')
const ctx = canvas.getContext('2d')

let angle = 0
const length_x = 100
const length_y = 100

function animate() {
  const x = canvas.width / 2 + length_x * Math.cos(angle)
  const y = canvas.height / 2 + length_y * Math.sin(angle)

  ctx.clearRect(0, 0, canvas.width, canvas.height)
  ctx.fillRect(x - 2, y - 2, 4, 4)

  angle += 0.01
  requestAnimationFrame(animate)
}

animate()