Algoritam za nalaženje stabilnih parova

Problem

Pretpostavimo da u jednom gradu na jugu Srbije imamo n mladića i n devojaka. Svi se međusobno znaju, jer je malo mesto. Svaki mladić ima rang listu svih devojaka iz mesta. Na prvom mestu se nalazi ona koja mu se najviše sviđa, a na poslednjem ona koja mu se sviđa najmanje. Sve devojke takođe imaju rang listu mladića. Te liste su nam unapred poznate na neki način (Radio Milevom).

Cilj nam je da uparimo momke i devojke tako da svi budu sretni, a da brakovi budu stabilni.

Skup brakova je stabilan ako ne postoji par mladić-devojka koji se jedno drugom sviđaju više nego njihovi bračni drugovi.

Na primer, pretpostavimo da su Marko i Jovana u jednom, a Petar i Milica u drugom braku. Na nesreću, Jovani se više sviđa Petar nego Marko, a Petru se sviđa više Jovana nego Milica. Ovo znači da bi Jovana i Petar bili srećniji da su zajedno. To može da bude razlog za brakolomstvo, pa se njihovi brakovi mogu smatrati nestabilnim. Matematički se može dokazati da uvek postoji stabilno uparivanje mladića i devojaka, takvo da ne postoji ni jedan nestabilan par.

Inače, algoritam su prvi put opisali D. Gale i L.S. Shapley 1962 godine.

Podaci

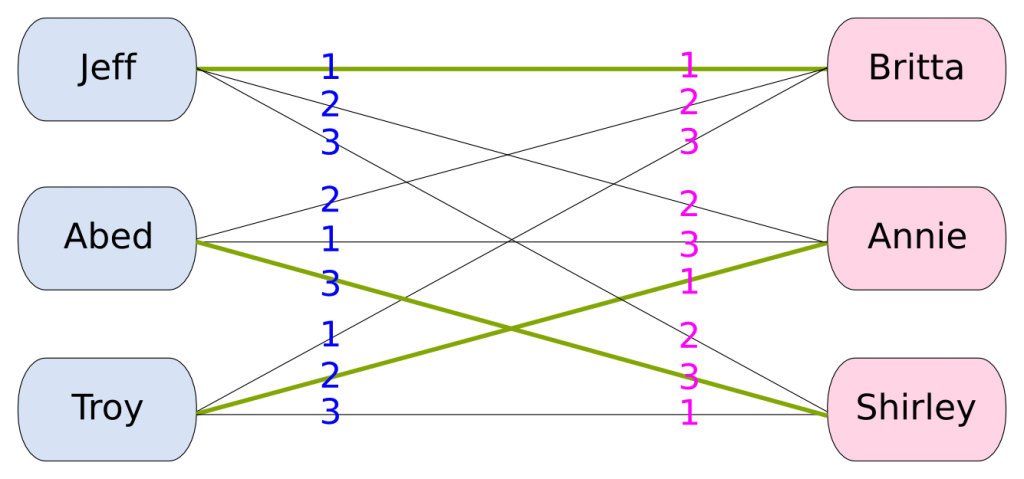
Hajdemo sada da problem razmotrimo na konkretnom slučaju 5 devojaka i 5 mladića. Mladiće ćemo označiti brojevima 1-5, a devojke slovim A-E.

Sledeća tabela pokazule njihove rang liste:

mladići ---------------------- devojke
C,B,E,A,D ------------ A: 3,5,2,1,4
A,B,E,C,D ------------ B: 5,2,1,4,3
D,C,B,A,E ------------ C: 4,3,5,1,2
A,C,D,B,E ------------ D: 1,2,3,4,5
A,B,D,E,C ------------ E: 2,3,4,1,5

Pokušajmo najpre jednu prostu (grabljivu) strategiju. Krenimo redom od prvog mladića i svima dajmo devojku koja je najviše kotirana na njegovoj listi, a još uvek je “raspoloživa”. To bi nam dalo sledeći rezultat uparivanja:

-- C
-- A
-- D
-- B
-- E

Da proverimo stabilnost ovako napravljenih parova.

Mladići 1, 2 i 3 su dobili svoje omiljene devojke, tako da im neće pasti na pamet da jure za drugima. Mladić 4 može biti problematičan jer mu se više sviđa devojka A od one koju je dobio (B), ali je devojka A njega stavila na poslednje mesto. Međutim njemu se više sviđa i devojka C one koju je dobio, a devojci C se on takođe više sviđa od onog kojeg je ona dobila (1). Znači mladić 4 i devojka C su potencijalni brakolomci. Uparivanje je, dakle, nestabilno.

Mogli bi sada da pokušamo da nekom kombinatorikom to popravimo, ali bi pri tom mogli da formiramo druge nestabilne parove i da, vrteći se u krug, ne nađemo rešenje. I to za samo 5 parova. A šta bi bilo da je 100-tinak ili više parova u pitanju? Izgleda kao nemoguć zadatak. Ali, generalno rešenje postoji i to veoma elegantno.

Algoritam

Sada ćemo opisati algoritam koji vodi do stabilnog uparivanja. Svakog dana se ponavlja sledeći scenario:

Jutro: Svaka devojka izađe na svoj balkon. Svaki mladić dođe ispod balkona devojke koja je na prvom mestu njegove rang liste i peva joj serenadu. Ako mladiću nije ostala ni jedna devojka u listi, on ostaje kod kuće ( i radi domaće zadatke iz programiranja).

Popodne: Svaka devojka koja ispod svog balkona ima udvarače, jednom od njih koji je najviši na njenoj rang listi kaže: “Možda, dođi sutra.”, a svim ostalima kaže: “Nikad se neću udati za tebe. Šetaj”.

Uveče: Svaki mladić koji je dobio “korpu” iz svoje liste briše devojku kod koje nema nikakve šanse.

Kada posle nekoliko dana ujutro ispod svakog balkona ostane samo po jedan mladić, devojke uzimaju te mladiće. Tako formirani parovi biće stabilni u skladu sa našom definicijom stabilnosti. Tu je i kraj našeg algoritma. Algoritam sadrži sve tri vrste koraka: sekvencu, selekciju i repeticiju.

Primena

Veoma je interesantno da ovaj algoritam u SAD-u ima jednu veoma praktičnu primenu. Tamo se svake godine svršeni studenti medicine upućuju na praksu u bolničke ustanove koje im najviše odgovaraju, upravo korišćenjem ovog algoritma.

Izvor: dr Milan Popović, Osnove programiranja (skripta)