Ređanje mehurom (bubble sort)

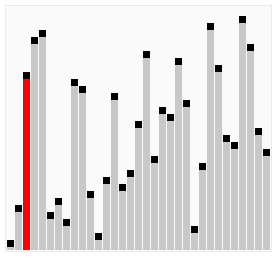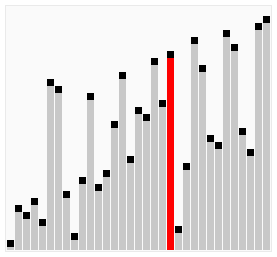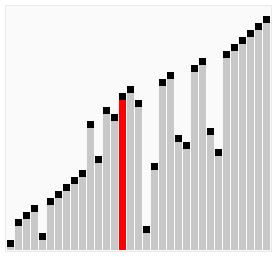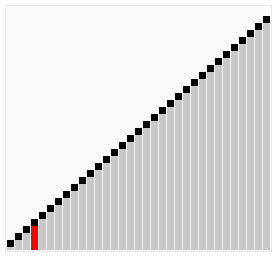
Ovo je jedna od najjednostavnijih metoda sortiranja koja je efikasna samo za relativno maleni broj elemenata. Za veći broj elemenata ova metoda je prespora. Stoga se vrlo retko upotrebljava osim za edukacijske svrhe.

Bubble sort algoritam u svakom prolazu kroz niz poredi susedne elemente, i zamenjuje im mesta ukoliko je potrebno. Prolasci kroz niz se ponavljaju sve dok se ne napravi prolaz u kome nije bilo razmene, što znači da je niz sortiran.

Primer

Prikažimo rad algoritma na primeru sortiranja niza (6 1 4 3 9):

Prvi prolaz:
(6 1 4 3 9) → (1 6 4 3 9), razmena jer je 6 > 1
(1 6 4 3 9) → (1 4 6 3 9), razmena jer je 6 > 4
(1 4 6 3 9) → (1 4 3 6 9), razmena jer je 6 > 3
(1 4 3 6 9) → (1 4 3 6 9)

Drugi prolaz:
(1 4 3 6 9) → (1 4 3 6 9)
(1 4 3 6 9) → (1 3 4 6 9), razmena jer 4 > 3
(1 3 4 6 9) → (1 3 4 6 9)
(1 3 4 6 9) → (1 3 4 6 9)

Treći prolaz:
(1 3 4 6 9) → (1 3 4 6 9)
(1 3 4 6 9) → (1 3 4 6 9)
(1 3 4 6 9) → (1 3 4 6 9)
(1 3 4 6 9) → (1 3 4 6 9)

Primetimo da je niz bio sortiran već nakon drugog prolaza, međutim, da bi se to utvrdilo, potrebno je bilo napraviti još jedan prolaz.

Naredna funkcija bubble sort algoritmom sortira niz a, dužine n.

void bubblesort(int a[], int n) {
  int bilo_razmene, i;
  do {
    bilo_razmene = 0;
    for (i = 0; i < n - 1; i++)
      if (a[i] > a[i + 1]) {
        razmeni(a, i, i+1);
        bilo_razmene = 1;
      }
  } while (bilo_razmene);
}

Uslov koji obezbeđuje parcijalnu korektnost je da ako bilo_razmene ima vrednost 0 pre provere uslova spoljašnje petlje, onda je niz a sortiran. Zaista, kada se spoljašnja petlja završi, vrednost promenljive bilo_razmene je 0, te prethodna implikacija obezbeđuje korektnost. Invarijanta unutrašnje petlje koja obezbeđuje pomenuti uslov je da ako promenljiva bilo_razmene ima vrednost 0, onda je deo niza a[0, i] sortiran. Zaista, po završetku unutrašnje petlje i ima vrednost n-1, te je pomenuti uslov obezbeđen.

Varijante

Svojstvo algoritma je da nakon svake iteracije spoljašnje petlje sledeći najveći elemenat koji nije bio na svojoj poziciji dolazi na nju. Bubble sort je na osnovu ovog svojstva i dobio ime (jer veliki elementi kao mehurići „isplivavaju“ ka kraju niza). Ovo sa jedne strane obezbeđuje zaustavljanje algoritma, dok se sa druge strane može iskoristiti za optimizaciju. Ovom optimizacijom se može smanjiti broj poređenja, ali ne i broj razmena.

void bubblesort(int a[], int n) {
  do {
    int i;
    for (i = 0; i < n - 1; i++)
      if (a[i] > a[i + 1])
        razmeni(a, i, i+1);
    n--;
  } while (n > 1);
}

Isti algoritam, može biti implementiran i na stilski malo drugačiji način (koji se može ponekad sresti u literaturi).

void bubblesort(int a[], int n) {
  int i, j;
  for (i = n - 1; i > 0; i--)
    for (j = 0; j < i; j++)
      if (a[j] > a[j + 1])
        razmeni(a, j, j+1);
}

Optimizacija može otići i korak dalje, ukoliko se dužina ne smanjuje samo za 1, već ukoliko se posmatra koliko je zaista elemenata na kraju niza već postavljeno na svoje mesto (ovo se može odrediti na osnovu mesta gde se dogodila poslednja zamena).

void bubblesort(int a[], int n) {
  do {
    int nn = 1, i;
    for (i = 0; i < n - 1; i++)
      if (a[i] > a[i + 1]) {
        razmeni(a, i, i+1);
        nn = i + 1;
      }
    n = nn;
  } while (n > 1);
}

U ovom slučaju, uslov koji važi pre provere uslova spoljašnje petlje je da su elementi od pozicije n-1 do kraja niza sortirani. Ovo obezbeđuje invarijanta unutrašnje petlje koja obezbeđuje da su svi elementi a[nn-1, i] sortirani.

Efikasnost

Što se efikasnosti tiče, najgori slučaj nastupa kada su elementi početnog niza sortirani u opadajućem poretku. U tom slučaju vrši se n prolaska kroz niz, a u svakom prolasku se pravi n poređenja i n razmena, što ukupno daje O(n^2) poređenja i O(n^2) razmena. Primetimo da se optimizacijom broj poređenja smanjuje oko dva puta.

Bubble sort algoritam se smatra veoma lošim algoritmom. Neki autori čak zagovaraju tezu da bi ga trebalo potpuno izbaciti iz nastave računarstva. U šali se navodi kako bi jedini gori algoritam bio onaj koji nasumično permutuje niz sve dok ne postane sortiran.

Izvor: Predrag Janičić i Filip Marić, PROGRAMIRANJE 2, Osnove programiranja kroz programski jezik C, Matematički fakultet, Beograd, 2017.