Sabiranje vektora

Vektore sabiramo tako što im saberemo svaku dimenziju ponaosob. Sabiranje 2D vektora:

a + b = [(a.x + b.x), (a.y + b.y)]

Sabiranje 3D vektora je identično, samo dodamo i treću dimenziju:

a + b = [(a.x + b.x), (a.y + b.y), (a.z + b.z)]

Ovako izgleda sabiranje 2d vektora sa pravim brojevima:

[0, 1] + [3, -2] = [(0 + 3), (1 - 2)] 
                 = [3, -1]

Primer: sabiranje vektora u kodu

const saberi = (v1, v2) => {
  return {
    x: v1.x + v2.x,
    y: v1.y + v2.y,
    z: v1.z + v2.z,
  }
}

const vektor1 = { x: 2, y: 1, z: 5 }
const vektor2 = { x: 5, y: 3, z: 3 }

console.log('Rezultat:', saberi(vektor1, vektor2))

Sabiranje vektora u igrama

Implementacija fizike u igrama jedan je od primera sabiranja vektora. Svaki fizički predmet obično ima vektore za položaj, brzinu i ubrzanje. Za svaki kadar, treba da integrišemo te vektore, tj. da dodamo brzinu položaju, i ubrzanje brzini.

Uzmimo na primer Super Marija koji skače. Njegova početna brzina skoka je (1,3), a ubrzanje (0,-1), jer ga gravitacija vuče naniže. Evo kako izgleda njegov skok tokom 8 kadrova:

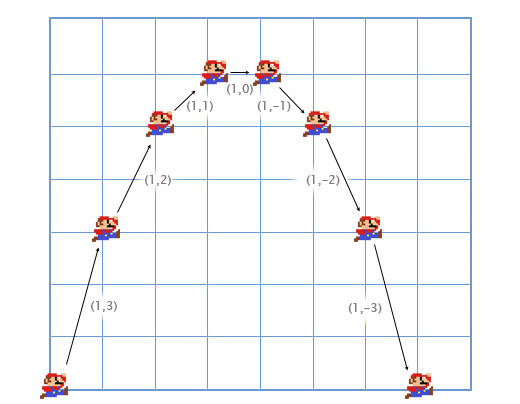
Kao što vidimo, u svakom kadru se dodaje gravitacija (-1) na njegovu vertikalnu brzinu. Obično igrač dodaje ubrzanje, a igra računa brzinu i položaj sabiranjem vektora.

Sabiranje vektora kao pomak

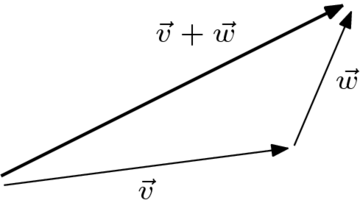
Možemo vizuelizovati sabiranje vektora kao pomeraj na mapi. Ako putujemo duž vektora v, a zatim skrenemo i pratimo vektor w, rezultat sabiranja vektora je pomeraj ili pomak vazdušnom linijom.

vector_addition

Sabiranje sila

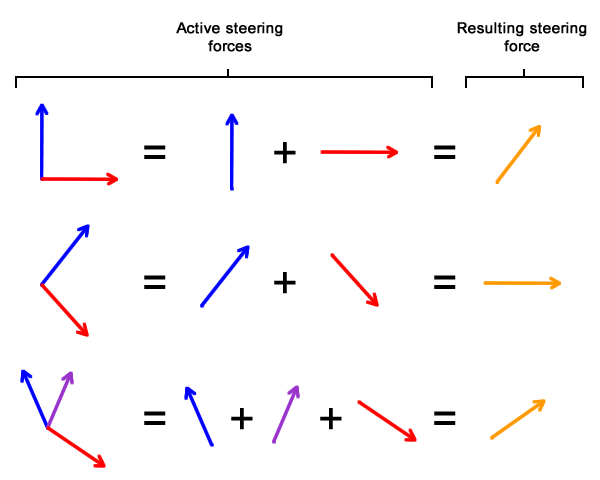
Sabiranjem vektora izračunavamo ukupnu silu (rezultantu) koja deluje na neki predmet:

sabiranje-vektora

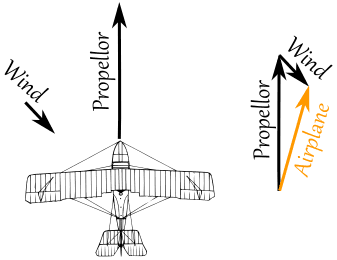
Na primer, ako avion ima pogon koji ga tera pravo, i naiđe na vetar koji ukoso duva u njega, sabiranjem dejstvujućih sila otkrivamo novu putanju aviona:

vector-airplane