Kako napraviti kružnu animaciju pomoću trigonometrije?

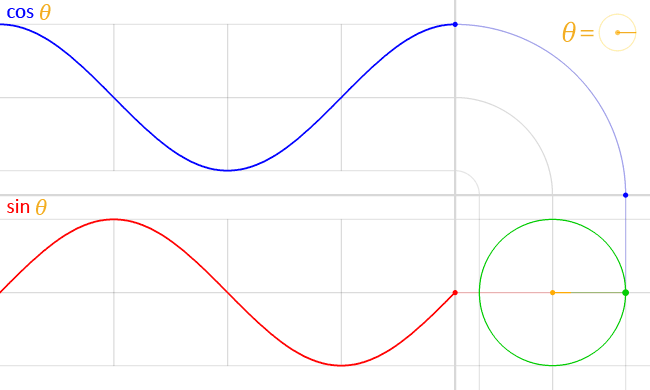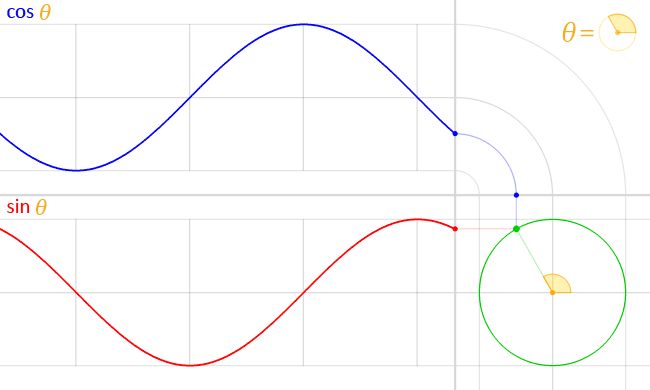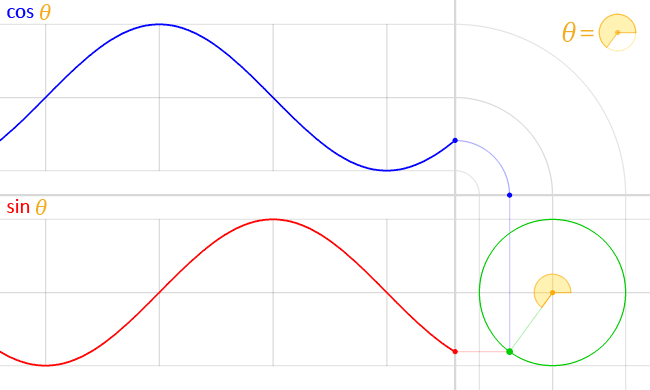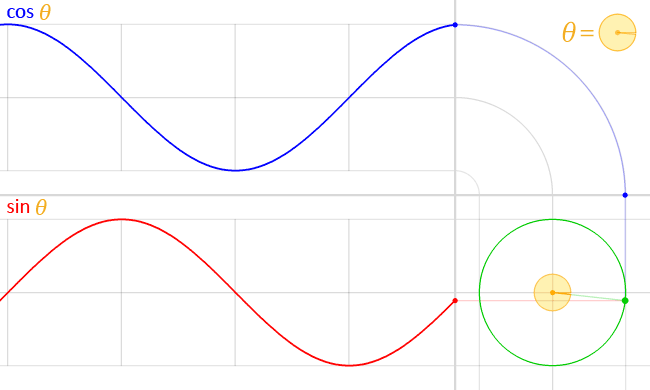
colors

Trigonometrijske funkcije, takođe nazvane kružne funkcije, su posebno korisne za modelovanje kružnog kretanja, talasa i drugih periodičnih pojava. Najpoznatije trigonometrijske funkcije su sinus i kosinus.

Uz njihovu pomoć lako možemo napraviti kružnu animaciju. Suština svega je u dve linije:

object.x = Math.cos(time)
object.y = Math.sin(time)

Obe funkcije, sin i cos, primaju jedan parametar (broj), a vraćaju rezultat između -1 i 1.

Korak 1: Trigonometrija ukratko

Trigonometrijske funkcije izvorno služe za računanje nepoznatih delova pravouglog trougla. Kada funkciji sin prosledimo ugao manji od 90° (jedan od dva oštra ugla), ona vrati odnos dve stranice (naspramna / najduža), kao decimal između 0 i 1. Npr, ako prosledimo ugao od 30° stepeni (PI/6 radijana), dobijemo da je odnos stranica 0.5:

sin(PI/6) => 0.5

Ovo još uvek nema nikakve veze sa animacijom.

No, trigonometrijske funkcije se koriste i za krugove. Uglovi van trougla, na primer na zidnom časovniku, mogu imati neograničeno veliku vrednost. U tom slučaju, funkcije sin i cos primaju bilo koji broj, pozitivni ili negativni, a vraćaju rezultat između -1 i 1.

Faktički, sinusoidne funkcije skaliraju bilo koji broj na vrednost između -1 i 1, i otprilike na svakih šest brojeva ponavljaju taj obrazac.

Rezultat se ciklično ponavlja na svaki pun krug, tj. na svakih 2 PI radijana (6.2831853, odnosno 360°), pa je rezultat sinusne funkcije sa ulazom n jednak rezultatu iste funkcije sa ulazom n + 2PI:

sin(n) = sin(n + 2PI)

Na primer, ako prvi put prosledite 14, a drugi put 14 + 6.2831853, dobićete isti rezultat. Slobodno probajte.

Korak 2: Praktična primena

Sada kada smo savladali osnovne pojmove, hajde da zavrtimo nešto. Za početak, da završimo birokratiju oko canvasa (pod pretpostavakom da ga imamo u HTML-u):

const canvas = document.getElementById('canvas')
ctx = canvas.getContext('2d')

Sada nam treba krug koji ćemo crtati, i funkcija koja ga crta:

const circle = {
  x: 100,
  y: 100,
  r: 25
}

const drawCircle = circle => {
  ctx.clearRect(0, 0, canvas.width, canvas.height)
  ctx.beginPath()
  ctx.arc(circle.x, circle.y, circle.r, 0, 2 * Math.PI)
  ctx.fill()
}

Konačno animacija:

const loop = () => {
    window.requestAnimationFrame(loop)
    const time = Date.now() / 1000
    circle.x = Math.cos(time)
    circle.y = Math.sin(time)
    drawCircle(circle)
}

loop()

Ili nee? Naš krug se trese zakucan u uglu. Hmm, opseg sin i cos funkcije je 2 (pixela), to nije dovoljno za animaciju. Hajde da dodamo modifikator:

const modifier = 100

Menjamo dva ključna reda:

circle.x = Math.cos(time) * modifier
circle.y = Math.sin(time) * modifier

Konačno imamo kružno kretanje, ali na pogrešnom mestu. Krug kruži oko ishodišta koordinatnog sistema, koje je u gornjem levom uglu. Hajde da ga pomerimo nadole i udesno (ponovo ažuriramo 2 ključne linije):

circle.x = Math.cos(time) * modifier + canvas.width / 2
circle.y = Math.sin(time) * modifier + canvas.height / 2

Kompletan primer

Eto, nije bilo toliko teško, imamo planetu koja kruži svemirom.

const canvas = document.getElementById('canvas')
const ctx = canvas.getContext('2d')
const modifier = 100

const circle = {
  x: 100,
  y: 100,
  r: 25
}

const drawCircle = circle => {
  ctx.clearRect(0, 0, canvas.width, canvas.height)
  ctx.beginPath()
  ctx.arc(circle.x, circle.y, circle.r, 0, 2 * Math.PI)
  ctx.fill()
}

const loop = () => {
    window.requestAnimationFrame(loop)
    const time = Date.now() / 1000
    circle.x = Math.cos(time) * modifier + canvas.width / 2
    circle.y = Math.sin(time) * modifier + canvas.height / 2
    drawCircle(circle)
}

loop()

Korak 3: Zabava

Hajde sada nešto da pokvarimo. Na primer da isključimo vodoravno kretanje, tj. zakomentarišemo x osu:

// circle.x = Math.cos(time) * modifier + canvas.width / 2

Pa da isključimo uspravno kretanje, odnosno y osu:

// circle.y = Math.sin(time) * modifier + canvas.height / 2

Vidimo da na ovaj načim dobijamo zanimljive efekte, odnosno razne vrste ravnomernog periodičnog kretanja, poput klatna.

Za kraj, malo sami eksperimentišite. Na primer, možete ubaciti još planeta koje imaju svoje orbite, možda i neke koje se vrte u suprotnom smeru.

Srećno kodovanje!

Bonus: napredna kružna animacija

Uz minimalne izmene izvornog koda možemo postići zanimljive efekte. Kod napredne animacije možete pogledati ovde.