Trigonometrijske funkcije

trigonometrijske-funkcije

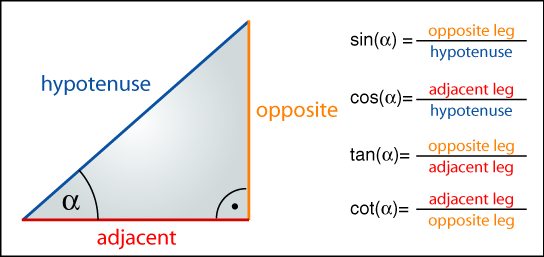
Trigonometrijske funkcije povezuju ugao pravouglog trougla sa odnosom dužina dve stranice. Mogu služiti za računanje nepoznatog ugla ili stranice trougla, a imaju i mnoge druge namene.

Koriste se i za krugove, jer oni imaju uglove i hipotenuzu (poluprečnik). Za razliku od trougla, ugao unutar kruga može iznositi bilo koju pozitivnu, pa čak i negativnu vrednost.

Formule

Najpoznatije trigonometrijske funkcije su sinus, kosinus i tangens:

sinus(α) = naspramna strana / hipotenuza  
kosinus(α) = ležeća strana / hipotenuza  
tangens(α) = naspramna / ležeća strana

Trigonometrijske formule možemo pamtiti po engleskim skraćenicama SOH, CAH, TOA:

sin(α) = opposite / hypotenuse
cos(α) = adjacent / hypotenuse
tan(α) = opposite / adjacent

Ove funkcije su ugrađene u digitrone i dostupne su u većini programskih jezika.

Sinus i kosinus

sin() i cos() se mogu koristiti za razne stvari. Obe funkcije primaju jedan parametar, ugao, i vraćaju broj između -1 i 1. Ugao može biti beskonačne veličine, ali se osnovni obrazac ponavlja svakih 360°.

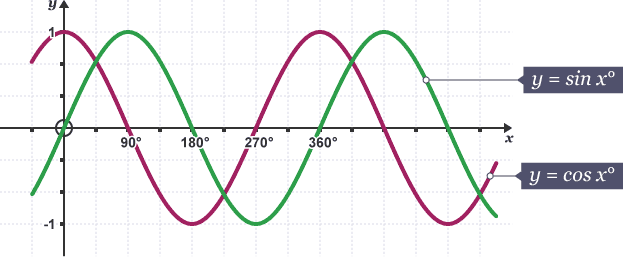
Primer: crtanje sinusne funkcije

JS program koji crta sinusnu funkciju:

const canvas = document.getElementById('canvas')
const ctx = canvas.getContext('2d')

const r = 60
const centerY = canvas.height / 2
let angle = 0
let animationId

ctx.beginPath()

function drawLine() {
    const x = angle / (2 * Math.PI) * 400
    const y = centerY - r * Math.sin(angle)
    ctx.lineTo(x, y)
    angle += 0.12
    ctx.stroke()
    if (angle < 2 * Math.PI)
        animationId = requestAnimationFrame(drawLine) 
    else
        cancelAnimationFrame(drawLine)
}

drawLine()

Tangens

Tangens je funkcija za izračunavanje odnosa naspramne i ležeće strane trougla, koje su označene sa y i x:

tan(α) = y / x

Tangens se može odrediti i ovako:

tan(α) = naspramna / ležeća = sin(α) / cos(α)

To znači da je tangens kombinacija sinus i kosinus funkcija.

Arktangens

Inverzne trigonometrijske funkcije služe da izračunamo nepoznati ugao trougla, na osnovu poznatih dužina dve stranice. Najkorisnija je inverzna funkcija tangensa, koja se zove arkus tangens ili arktangens:

ugao = atan(naspramna / ležeća strana)

U slučaju negativnih vrednosti daje netačan rezultat, jer dva suprotna vektora imaju isti odnos dve stranice.

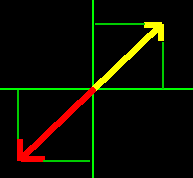
Delimično rešenje je moguće ovako (delimično jer ne proveravamo slučaj kada x je 0):

if (x > 0)
    angle = atan(y / x)
else
    angle = PI + atan(y / x)

Da bi se stvari pojednostavile, funkcija atan2() je dostupna u većini programskih jezika:

angle = atan2(y / x)