Deo zbornika Teorija razvoja igara

Vektorski proizvod

Vektorski proizvod (ili unakrsni proizvod) je operacija između dva vektora u 3D prostoru koja rezultira novim vektorom, normalnim na oba.

Operacija se obeležava znakom ×:

a × b

Komponente rezultirajućeg vektora računamo na sledeći način:

• x = (a.y * b.z) - (a.z * b.y)
• y = (a.z * b.x) - (a.x * b.z)
• z = (a.x * b.y) - (a.y * b.x)

Redosled je bitan

Redosled činilaca je bitan jer vektorski proizvod nije komutativan:

a × b != b × a

Rezultirajući vektor ima uvek istu veličinu i normalan je na oba činioca, li mu smer zavisi od redosleda:

• Ako je redosled a × b, rezultat će biti u pravcu desne ruke.
• Ako je redosled b × a, rezultat će biti u suprotnom pravcu.

Smer rezultirajućeg vektora možemo vizuelizovati na sledeći način:

Rotiranje vektora u 2D igrama

Recimo da imamo brod sa topovima bočno. Ako je brod okrenut u smeru (2,1), gde su okrenuti topovi? Ovo je prosto u 2D. Da bi rotirali vektor za 90 stepeni u smeru kazaljke, prvo zamenimo mesta komponentama, te predznak druge komponente. Tako (a,b) postaje (b,-a). Dakle, ako je brod okrenut u smeru (2,1), desni topovi su okrenuti u smeru (1,-2). Levi topovi su suprotni, dakle menjamo predznake oba broja: (-1,2).

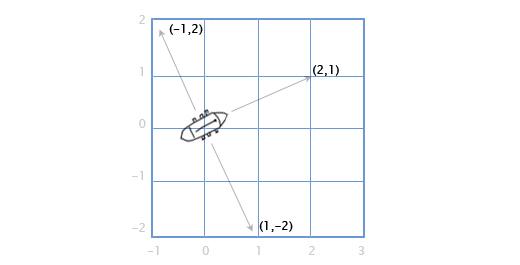
Objašnjenje

Za rotiranje vektora za 90 stepeni (u smeru kazaljke), koristimo sledeću 2D rotacionu matricu:

R(90°) = |  0  1 |
         | -1  0 |

Kada pomnožimo rotacionu matricu sa vektorom (a, b) koristeći množenje matrica, dobijamo:

v' = |  0  1 |   *   | a |
     | -1  0 |       | b |
   = | ( 0 * a + 1 * b)  |
     | (-1 * a + 0 * b)  |
   = (b, -a)

Dakle, vektor (a, b) nakon rotacije za 90 stepeni postaje (b, -a).

Vektorski proizvod u 3D igrama

Recimo da imamo jedrenjak sa jarbolom M okrenutim nagore (0,1,0), i vetar W u smeru (1,0,2). Želimo jedro S da usmerimo da što bolje uhvati vetar, tj. da bude normalno i na jarbol i na vetar.

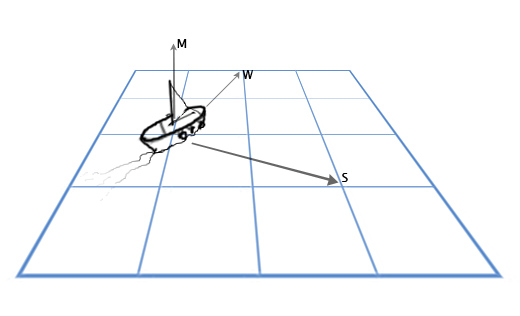
Da bismo rešili ovo, koristimo vektorski proizvod:

S = M × W
  = (0, 1, 0) × (1, 0, 2) 
  = (1*2 - 0*0, 0*1 - 0*2, 0*0 - 1*1) 
  = (2, 0, -1)

Ovo naravno nećemo uvek raditi ručno. Za ubuduće, najbolje je vektorski proizvod enkapsulirati u funkciju:

function cross(a, b) {
    return {
        x: a.y * b.z - a.z * b.y,
        y: a.z * b.x - a.x * b.z,
        z: a.x * b.y - a.y * b.x
    }
}