Deo zbornika Učimo strukture podataka

Stog (stack)

Stog ili plast (en. stack) je linearna struktura podataka, gde se elementi mogu dodavati ili oduzimati samo na jednom kraju. Nazvana je po plastu, gde se seno uvek dodaje i oduzima samo s vrha.

Nizovi i liste dozvoljavaju dodavanje i brisanje elemenata na bilo kojem mjestu – početku, kraju ili između. Postoje određeni scenariji kada želimo ograničiti dodavanja i brisanja elemenata samo na jedan kraj liste.

Drugi uobičajeni naziv za ovu strukturu je LIFO lista (eng. last in – first out).

Osnovne operacije

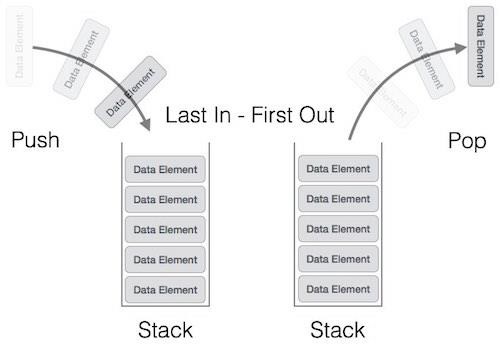
Osnovne operacije na stogu su:

• dodavanje elementa na stog (eng. push)
• uklanjanje elementa iz stoga (eng. pop)

Nije moguće izvaditi ili umetnuti bilo koji element iz sredine prije nego se “skinu” svi elementi iznad njega. Iz toga slijedi da je zadnji dodani element ujedno i onaj koji će se prvi izvaditi. Drugim riječima stog je struktura kod koje se posljednji pohranjeni podatak prvi uzima u obradu.

Operacija dodaj ili briši zahtijeva jednako vremena bez obzira na broj pohranjenih podataka.

Premda se čini da je stog vrlo restriktivna struktura podataka, on ima brojne vrlo važne primjene u računalnoj znanosti. Često se upotrebljava u situacijama kada određene korake obrade treba odgoditi do trenutka ispunjenja drugih uvjeta.

Implementacija

Sledi prosta implementacija stoga u Javascriptu:

stog = []
stog.push(2)             // stog je sada [2]
stog.push(5)             // stog je sada [2, 5]
element = stog.pop()     // stog je sada [2]
console.log(element)     // stampa 5

Malo naprednija implementacija, sa klasom omotačem, izgledala bi otprilike ovako:

class Stog {
    constructor() {
      this.niz = []
    }

    dodaj(el) {
        this.niz.push(el)
    }

    ukloni(){
        return this.niz.pop()
    }
}

stog = new Stog
stog.dodaj(2)             // stog je sada [2]
stog.dodaj(5)             // stog je sada [2, 5]
element = stog.ukloni()   // stog je sada [2]
console.log(element)      // stampa 5

Prelivanje steka (stack overflow)

Prelivanje steka (stack overflow) je greška koja nastaje kada program pređe ograničenje memorije dodeljene steku (posebnoj oblasti memorije za čuvanje lokalnih promenljivih i povratnih adresa funkcija).

Obično nastaje kada funkcije pozivaju jedna drugu ili same sebe (rekurzija) bez pravilnog završetka, ili kada lokalni podaci u funkciji zauzmu više prostora nego što stek može da podrži.

Literatura

• N. Pavković, D. Marjanović, N. Bojčetić, Programiranje i algoritmi II, Zagreb, 2005.
• Petlja.org, Strukture podataka