Vrste grafova

Graf u kojem postoji bar jedan put od svakog čvora do bilo kojeg drugog čvora naziva se povezan graf.

Jednostavan graf nema višestruke grane između čvorova ni petlje. Opšti graf može imati višestruke grane između čvorova i petlje.

Usmjereni graf je graf u kojem svaka ivica ima smjer. U usmjerenom grafu dve ivice suprotnih smjerova mogu povezivati iste čvorove.

Ako svakoj ivici pripada neki podatak, graf se naziva označenim. Ako su ivicama pridružene numeričke vrijednosti, graf se naziva težinskim.

Potpun graf

Potpun graf je najgušći jednostavan graf (sa najvećim mogućim brojem grana), tj. koji ima granu između svaka dva čvora. Ako želimo da izračunamo broj grana nekog potpunog grafa koristimo formulu E = V * (V – 1) / 2, gdje je E traženi broj grana, a V broj čvorova u tom grafu.

Ovaj algoritam kreira kompletan graf, odnosno sve moguće ivice za data čvorove:

const povezi = cvorovi => {
  const grane = []
  for (let i = 0; i < cvorovi.length; i++)
    for (let j = 0; j < cvorovi.length; j++)
      if (j > i)
        grane.push([cvorovi[i], cvorovi[j]])

  return grane;
}

const cvorovi = ['A', 'B', 'C']
console.log(povezi(cvorovi))
✎

Stablo

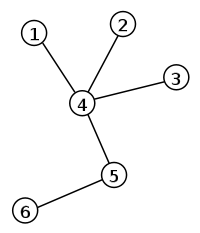
Nasuprot potpunom, najređe povezan graf naziva se stablo. Dakle, stablo je povezani graf koji ima minimalan mogući broj grana. Ako stablo ima V čvorova, broj grana u njemu je E = V – 1.

Nepovezan graf

Svaki povezani graf sastoji se obavezno iz samo jedne povezane komponente, dok se svaki nepovezan graf sastoji iz više povezanih komponenti. Na primer, neki graf se sastoji iz dvije grupe čvorova (dvije povezane komponente), ali između njih ne postoji nikakva grana koja ih spaja.

Karakteristika povezanih grafova je da iz svakog čvora postoji barem jedan put do bilo kojeg drugog čvora, dok je kod nepovezanih grafova iz nekih čvorova nemoguće stići do nekih drugih.

Izvori

N. Pavković, D. Marjanović, N. Bojčetić, Programiranje i algoritmi II, Zagreb, 2005.
Uvod u teoriju grafova