Deo zbornika Učimo strukture podataka

Operacije nad matricama

Matrice se mogu sabirati, množiti, transponovati i invertovati.

Matrične operacije se često koriste u razvoju igara. Na primer, množenje matrica može se koristiti za izračunavanje kretanja objekata, a transponiranje za izračunavanje rotacija ili transformacija objekata.

Sabiranje i oduzimanje matrica

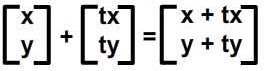
Matrice istih dimenzija se mogu sabirati. Sabiranje matrica vrši se tako što sabiramo elemente na istim pozicijama iz obe matrice. Oduzimanje matrica radi na isti način, samo oduzimamo pripadajuće elemente.

Sabiranje matrica u C++

Ova funkcija sabira dve matrice 3x3:

Matrix3X3 addMatrices(Matrix3X3 a, Matrix3X3 b)
{
  Matrix3X3 newMatrix;
  for(int i=0; i<3; i++)
    for(int j=0; j<3; j++)
      newMatrix[i][j] = (a[i][j] + b[i][j]);

  return newMatrix;
}

Množenje matrica

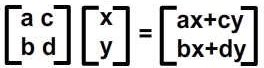
Množenje matrica moguće je samo ako je broj kolona prve jednak broju redova druge. Rezultat je nova matrica koja ima redova koliko prva, a kolona koliko druga matrica.

Matrice A i B množimo tako što računamo skalarni proizvod svake kolone A i svakog reda B.

Za matrice ne važi komutativnost množenja: A x B != B x A.

Primer množenja

Matrica A (2x3):

1  2  3  
4  5  6  

Matrica B (3x2):

7  8  
9  10  
11 12  

Procedura:

(1,2,3) • (7,9,11)  = (1*7) + (2*9)  + (3*11) = 58  
(1,2,3) • (8,10,12) = (1*8) + (2*10) + (3*12) = 64  
(4,5,6) • (7,9,11)  = (4*7) + (5*9)  + (6*11) = 139  
(4,5,6) • (8,10,12) = (4*8) + (5*10) + (6*12) = 154  

Rezultat (2x2):

58  64  
139 154  

Množenje matrica u C++

Ova funkcija množi dve matrice 3x3:

Matrix3X3 multiply3X3Matrices(Matrix3X3 a, Matrix3X3 b) {
  Matrix3X3 newMatrix;
  for (int i = 0; i < 3; i++) {
    for (int j = 0; j < 3; j++) {
      for (int k = 0; k < 3; k++) {
        newMatrix[i][j] += (a[i][k] * b[k][j]);
      }
    }
  }
  return newMatrix;
}

Množenje matrica u JS-u

Standardni algoritam za množenje matrica, koji ima vremensku složenost O(n³):

function multiplyMatrices(a, b) {
  const rowsA = a.length
  const colsA = a[0].length
  const colsB = b[0].length

  const newMatrix = Array.from({ length: rowsA }, () => Array(colsB).fill(0))
  
  for (let i = 0; i < rowsA; i++)
    for (let j = 0; j < colsB; j++)
      for (let k = 0; k < colsA; k++)
        newMatrix[i][j] += a[i][k] * b[k][j]

  return newMatrix
}

// upotreba
const matricaA = [[1, 2, 3], 
                  [4, 5, 6]]

const matricaB = [[7, 8], 
                  [9, 10],
                  [11, 12]]

console.log(multiplyMatrices(matricaA, matricaB))

Funkcionalna verzija bi izgledala ovako:

const transpose = a => a[0].map((x, i) => a.map(y => y[i]))
const dotProduct = (a, b) => a.map((x, i) => a[i] * b[i]).reduce((m, n) => m + n)
const multiplyMatrices = (a, b) => a.map(x => transpose(b).map(y => dotProduct(x, y)))

// upotreba
const matricaA = [[1, 2, 3], 
                  [4, 5, 6]]

const matricaB = [[7, 8], 
                  [9, 10],
                  [11, 12]]

console.log(multiplyMatrices(matricaA, matricaB))

Transponovanje matrica

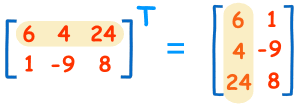
Transponovanje je zamena redova i kolona matrice. To znači da će elementi koji su bili u istom redu biti u istoj koloni, a elementi koji su bili u istoj koloni biti u istom redu. Na primer, ako imamo matricu od 2 reda i 3 kolone, njena transponovana matrica će imati 3 reda i 2 kolone.

Transponovana matrica A se označava kao AT.

Transponovanje matrica u C++

Matrix4X4 transpose4X4Matrix(Matrix4X4 a) {
  Matrix4X4 newMatrix;
  for (int i = 0; i < 4; i++) {
    for (int j = 0; j < 4; j++) {
      newMatrix[i][j] = a[j][i];
    }
  }
  return newMatrix;
}

Transponovanje matrica u JS-u

const transpose = a => a[0].map((x, i) => a.map(y => y[i]))

console.log(transpose([
  [3, 2], 
  [5, 6], 
  [7, 8]
]))

Invertovanje

Invertovanje matrice je operacija koja se primenjuje na kvadratne matrice da bi se dobila inverzna matrica. Inverzna matrica, kada se pomnoži sa izvornom matricom, daje jediničnu matricu:

A × A⁻¹ = I

Ne mogu se sve matrice invertovati. Matrice koje se ne mogu invertovati nazivaju se singularne matrice.

Postupak invertovanja matrice može biti složen, ali postoje programi koji ga automatizuju.